基本介紹
- 中文名:小數部分函式
- 外文名:decimal part function
- 別名:分數部分函式
- 屬性:一種特殊的數論函式
- 符號:{x}
基本介紹
取整函式







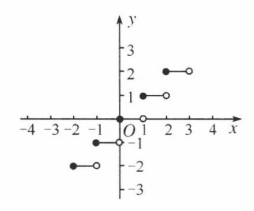
小數部分函式




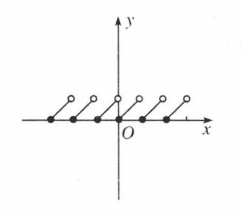




相關性質

























初等函式與非初等函式
初等函式

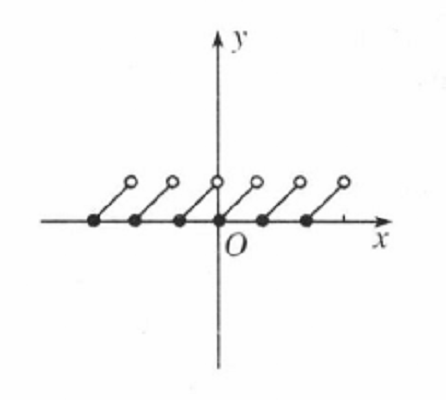











































小數部分函式(decimal part function)亦稱分數部分函式,是一種特殊的數論函式。x的小數部分記為{x},讀作x的小數部分(或分數部分)。小數部分函式被定義為{x}=x-[x],其中[x]是整數函式。{x...
函式使用用法 根據Excel的幫助得知,round函式就是返回一個數值,該數值是按照指定的小數位數進行四捨五入運算的結果。round函式的語法是:ROUND(number,num_digits),即:Round(數值,保留的小數位數)Number:需要進行四捨五入的數字。Num_digits:指定的位數,按此位數進行四捨五入。其中,如果 num_digits 大於 0...
TRUNC函式是將數字的小數部分截去,返回數字的整數部分。它的語法格式為TRUNC(number,number_digits),其中number為需要截尾取整的數字,number_digits為指定取整精度的數字,默認為0。例如函式TRUNC(8.5)的返回值是8,而TRUNC(-8.5)的返回值為-8。雖然這兩個函式是取整函式,但是它們的算法是不一樣的。INT...
形如y=a{x/b}(b≠0)的函式叫做餘數函式,即x除a的餘數。也記做xmodb,讀作x余b。定義 {a.b}[a.b]的意義 {a.b}是指a.b的小數部分;[a.b]指a.b的整數部分,a.b={a.b}+[a.b]若a.b ≧0,則{a.b}=0.b,[a.b]=a 若a.b ≦0,則{a.b}=1-0.b,[a.b]=a-1 性質 方程與不...
Microsoft Excel for Windows 和 Microsoft Excel for the Macintosh 使用不同的默認日期系統。時間值為日期值的一部分,並用小數來表示(例如 12:00 PM 可表示為 0.5,因為此時是一天的一半)。示例 其他信息 PHP time() 函式 定義和用法 time() 函式返回當前時間的 Unix 時間戳。語法 time(void)技術細節 說...
函式語法 返回Variant(String),其中含有一個表達式,它是根據格式表達式中的指令來格式化的。語法 Format函式的語法具有下面幾個部分:設定值 firstdayofweek參數有下面設定:firstweekofyear參數有下面設定:說明 如果在格式化數字時沒有指定format,Format會提供與Str函式類似的功能,儘管它是國際化的。然而,以Format作用...
注意 CLng 函式與 Fix 和 Int 函式功能不同,後兩者函式對數值的小數部分進行截尾取整而不是四捨五入。當小數部分恰好等於 0.5 時, CLng 函式通常向與此數最接近的偶數取整。例如,0.5 取整為 0、1.5 取整為 2。
貌似沒有這函式。我們擁有下面這個 "Products" 表:我們希望顯示當天的日期所對應的名稱和價格。我們使用如下 SQL 語句:SELECT ProductName, UnitPrice, Now() as PerDate FROM Products結果集類似這樣:ROUND()ROUND 函式用於把數值欄位捨入為指定的小數位數。SELECT ROUND(column_name,decimals) FROM table_name "...
trunc是一種函式,功能和函式INT類似,是截取日期或數字,返回指定的值。函式trunc直接去除數字的小數部分,而函式INT則是向下捨入到最接近的整數。語法 TRUNC(number,num_digits)Number 需要截尾取整的數字。Num_digits 用於指定取整精度的數字。Num_digits 的默認值為 0。說明 函式 TRUNC 和函式 INT 類似,都返回...
modf,多義詞,一、c語言的數學函式 二、醫學專用名詞,在醫學中指多器官功能障礙綜合症。數學函式 函式名:modf 頭檔案:函式原型:double modf(double x, double *ipart)函式用途:分解x,以得到x的整數和小數部分 輸入參數:x 待分解的數輸出參數:ipath x 的整數部分 返回值:x 的小數部分 實例代碼:運行...
對SQL Server而言,Decimal可用來保存具有小數點而且數值確定的數值,它不像float和real是用來保存近似值。對於Visual Basic而言,Decimal是其版本5新增的數據類型,目的是滿足進行精密數學運算的需求,它是範圍最大、最精確的浮點數類型。對於Excel而言,DECIMAL()函式用於按給定基數將數字的文本表示形式轉換成十進制數。...
函式名: ceil 用 法: double ceil(double x);功 能: 返回大於或者等於指定表達式的最小整數 頭檔案:math.h 說明:float ceil ( float value )返回不小於 value 的下一個整數,ceil() 返回不小於value的最小整數,value 如果有小數部分則進一位。ceil() 返回的類型仍然是 float,因為 float 值的範圍通常比...
strtof是指向的如果不是一個空指針,功能上也endptr指向的值設定為指向的第一個字元的數量後, 該函式首先丟棄許多空白字元。函式原型 float strtof(const char *nptr, char **endptr);endptr endptr指向的如果不是一個空指針,功能上也endptr指向的值設定為指向的第一個字元的數量後, 該函式首先丟棄許多空白...
format-number() 函式用於把字元串轉換為數字。語法 FormatNumber(expression [,NumDigitsAfterDecimal [,IncludeLeadingDigit [,UseParensForNegativeNumbers [,GroupDigits]]])Arguments Expression 必選項。要被格式化的表達式。NumDigitsAfterDecimal 可選項。指示小數點右側顯示位數的數值。默認值為 -1,指示使用的是計算...
其一是利用Round函式對小數進行精確的四捨五入,其格式為:round(number,num_digits),其中“number” 為需要四捨五入的數字或運算公式,num_digits指定四捨五入的位數。針對本文所述問題,我們只需在D2單元格中輸入“=Round((B2+C2)*0.11,2)”,在“E2”單元格中輸入“=Round(D2*3.12,2)”即可。另...
3 、雙曲三角函式 double sinh (double);double cosh (double);double tanh (double);4 、指數與對數 double frexp(double value,int *exp);這是一個將value值拆分成小數部分f和(以2為底的)指數部分exp,並返回小數部分f,即f*2^exp。其中f取值在0.5~1.0範圍或者0。double ldexp(double x,int exp)...
應該使用數據類型轉換函式來代替Val,以使國際版的數據轉換可以從一種數據類型轉換為另一種。例如,當使用Ccur時,不同的小數點分隔設定、千分位分隔設定和各種貨幣選項,依據系統的國別設定都會被妥善識別。當小數部分恰好為 0.5 時,Cint和CLng函式會將它轉換為最接近的偶數值。例如,0.5 轉換為 0、1.5 轉換為 2...
