基本介紹
- 中文名:對偶命題
- 外文名:dual propositions
- 所屬學科:數學
- 定義:指成對偶對應的幾何命題
- 相關概念:對偶原則、射影平面、對偶元素等
定義
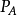
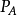
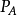
詳細介紹
舉例
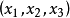
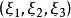
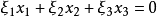
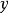
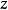
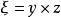
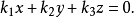
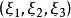
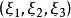
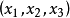
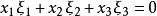
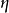
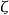
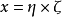
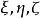
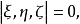
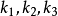


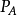
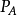
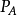
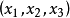
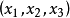
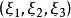
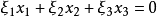
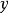
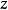
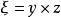
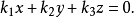
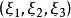
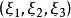
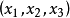
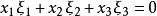
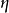
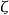
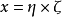
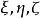
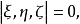
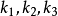

對偶命題是具有特定關係的兩個命題,指成對偶對應的幾何命題。射影幾何中一個命題與把其中的各個幾何元素換成對偶元素,把其中的各個運算換成對偶運算而得到的另一...
自對偶命題(self-dual propositions )是一種特殊的對偶命題,即意義一致的兩個命題。例如,“三點及其兩兩連線組成一個三點形”與“三線及其兩兩交點組成一個三線...
對偶元素是射影幾何的一個術語,指射影幾何中元素間的一種特殊關係。在歐氏幾何中,幾何圖形是點的軌跡,是把點作為圖形基本元素,而射影幾何認為圖形可看成是直線...
對偶原則,又稱為對偶原理。是射影幾何的一個基本原則,指在射影空間中,若一個命題成立,則其對偶命題也必成立。...
將∪ 和∩,或者 Ø 和 U 相互交換,一個恆等式就變成了相應的另一個。 這是集合代數的一個非常重要的性質,稱作集合的對偶性原理。它對集合的所有真命題...
對偶原理,又叫對偶原則。對偶原理是指在射影空間中,若一個命題成立,則其對偶命題也必成立。...
例如,兩點連線中點改成直線,直線改成點得到:兩直線交點;又例如,三點共線改成三直線共點,這樣改變以後得到一個新的射影幾何命題,稱為原命題的對偶命題,下面是...
1 定理定義 2 驗證推導 3 對偶命題 4 定理推廣 帕普斯定理定理定義 編輯 帕普斯(Pappus)定理:如圖,直線l1上依次有點A,B,C,直線l2上依次有點D,E,F,設...
在射影平面上,如果一個命題成立,那么它的對偶命題也成立,這叫做平面對偶原則。同樣,在射影空間裡,如果一個命題成立,那么它的對偶命題也成立,叫做空間對偶原則。...
這兩個命題叫做對偶命題。這就是射影幾何學所特有的對偶原則。在射影平面上,如果一個命題成立,那么它的對偶命題也成立,這叫做平面對偶原則。同樣,在射影空間裡,...
例如,兩點連線中點改成直線,直線改成點得到:兩直線交點;又例如,三點共線改成三直線共點,這樣改變以後得到一個新的射影幾何命題,稱為原命題的對偶命題,下面是...
