射影運算元(projection operator) S'=R/2}Z上零階擬微分運算元.
射影運算元
相關詞條
- 投影運算元
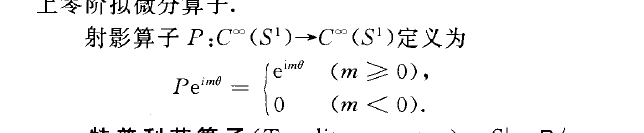
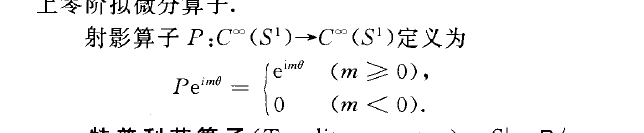
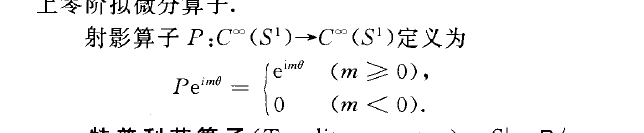
投影運算元是在賦范線性空間X上具有冪等性的有界線性運算元。設P是X上的有界線性運算元,如果P2=P,則稱P為投影運算元。當P是投影運算元時,I-P也是投影運算元,且X=PX+(...
- 射影運算元
射影運算元(projection operator) S'=R/2}Z上零階擬微分運算元. ... 射影運算元(projection operator) S'=R/2}Z上零階擬微分運算元.詞條標籤: 人物 ...
- 正交投影運算元
,定義運算元P如下:Px=x1,即Px是x在M上的投影,稱運算元P為由H到M上的正交(或直交)投影運算元,簡稱投影(或射影)運算元。正交投影運算元性質 編輯 投影運算元P具有下列性...
- 微分法
其中的 是 -射影運算元,也就是說將一個向量 射到它的第 個分量 的映射。而 是滿足:的k-形式。特別地,當 是一個從 映射到 的函式時,可以將 寫作:...
- 伯格曼投影
表示了希爾伯特空間L2(D)到伯格曼空間的正交投影運算元,P稱為伯格曼投影,其中K(z,w)為再生核,顯然它是有界運算元。伯格曼投影性質 編輯 一般...
- 完全對稱化子
x∈H,必有分解x=x1+x2,x1∈M,x2∈M,定義運算元P如下:Px=x1,即Px是x在M上的投影,稱運算元P為由H到M上的正交(或直交)投影運算元,簡稱投影(或射影)運算元。
- 擴張性質
巴拿赫空間Y具有擴張性質的充分必要條件是:對於任何包含Y為其賦范線性子空間的每個賦范線性空間Y0,都存在一個由Y0到Y的範數為1的射影運算元。
- 無限投影
無限投影是馮·諾伊曼代數中的一類投影運算元。設P是馮·諾伊曼代數𝓜中的投影,P稱為是無限的,如果代數𝓜P=P𝓜P是無限的。 [1] ...
- 譜論
若E是從B到巴拿赫空間X上射影運算元族之同態映射,並且E(·)還是一致有界的,即E(C)=I,E(C\σ)=I-E(σ),‖E(σ)‖≤K(常數) (σ∈B),則稱{E(σ...
- 維納一霍普夫分解
維納一霍普夫分解(Wiener - Hopf factoriza -tion)運算元的一種分解式.設A是希爾伯特空間H中的線性運算元,p.是投影運算元,A的維納一霍普夫分解是指分解式A=A_A+, ...
- 曾遠榮
尤其對兩種連續譜運算元都運用黑林格(Hellinger)積分為射影運算元。而在此之前,即使在可分的希爾伯特(Hilbert)空間中有界埃爾米特變換的研究中,也沒有出現三部分解。
- 泛函分析(第2版)
第四章 有界線性運算元譜論 1. 有界線性運算元的譜 2. 射影運算元與約化 3. 緊運算元 4. 有界自伴運算元 5. 有界自伴運算元的譜測度與函式演算 6. 酉運算元 第五...
- 純無限投影
純無限投影是馮·諾伊曼代數中的一類投影運算元。設P是馮·諾伊曼代數𝓜中的投影,P稱為是純無限的,如果代數𝓜P=P𝓜P是純無限的。 [1] ...
- 泛函分析/新世紀高等學校教材(第二版)
§2.6 射影極限§2.7 歸納極限第三章 線性運算元理論的基本定理§3.1 線性運算元的連續性和有界性的關係§3.2 閉圖像定理.§3.3 等度連續性定理....
- 空間和變換
7.3 投影運算元和投影矩陣 第八章 三維空間中的剛體運動 8.1 三維歐氏空間上的剛體運動 8.2 剛體變換的表示 8.3 坐標和速度的變換 第九章 三維空間中剛...
- 魯棒自適應控制及其航空航天套用
11.4射影運算元 11.5基於射影理論的MRAC設計 11.6總結 11.7習題 [1] 參考文獻 第12章基於近似的自適應系統 12.1研究目的 12.2基本定義 12.3前饋神經網路...
- 現代數學基礎:泛函分析中的反例
6.存在範數不等於1的射影運算元 7.Hahn—Banach定理不能推廣到一般的有界線性運算元 8.存在某個Banach空間上的非零連續線性泛函,它在單位閉球上取不到最大值 ...
