基本介紹
- 中文名:完全四線形
- 外文名:Complete quadrangle
簡介,歐幾里得空間,射影幾何,完全四邊形,
簡介
在數學,尤其是射影幾何學里,完全四線形是指歐幾里德平面上由四條兩兩相交但是任意三條不共點的直線加上它們的六個交點組成的圖形。相應地,由四個三三不共線的點加上它們之間的六條連線所構成的圖形則稱為完全四點形。
歐幾里得空間
歐幾里得幾何是在約公元前300年,由古希臘數學家歐幾里得建立的角和空間中距離之間聯繫的法則。歐幾里得首先開發了處理平面上二維物體的“平面幾何”,他接著分析三維物體的“立體幾何”,所有歐幾里得的公理被編排到幾何原本。
這些數學空間可以被擴展來套用於任何有限維度,而這種空間叫做 n維歐幾里得空間或有限維實內積空間。這些數學空間還可被擴展到任意維的情形,稱為實內積空間(不一定完備),希爾伯特空間在高等代數教科書中也被稱為歐幾里得空間。 為了開發更高維的歐幾里得空間,空間的性質必須非常仔細的表達並被擴展到任意維度。 儘管結果的數學非常抽象,它卻捕獲了我們熟悉的歐幾里得空間的根本本質,根本性質是它的平面性。 另外儲存在其他種類的空間,例如球面非歐幾里得空間,相對論所描述的四維時空在重力出現的時候也不是歐幾里得空間。
射影幾何
在數學里,射影幾何(projective geometry)研究在射影變換下不變的幾何性質。與初等幾何不同,射影幾何有不同的設定、射影空間及一套基本幾何概念。直覺上,在一特定維度上,射影空間比歐氏空間擁有“更多”的點,且允許透過幾何變換將這些額外的點(稱之為無窮遠點)轉換成傳統的點,反之亦然。
射影幾何中有意義的性質均與新的變換概念有關,此一變換比透過變換矩陣或平移(仿射變換)表示的變換更為基礎。對幾何學家來說,第一個問題是要找到一個足以描述這個新的想法的幾何語言。不可能在射影幾何內談論角,如同在歐氏幾何內談論一般,因為角並不是個在射影變換下不變的概念,如在透視圖中所清楚看到的一般。射影幾何的許多想法來源來自於對透視圖的理論研究。另一個與初等幾何不同之處在於,平行線可被認為會在無窮遠點上交會,一旦此一概念被轉換成射影幾何的辭彙之後。這個概念在直觀上,正如同在透視圖上會看到鐵軌在水平線上交會一般。有關射影幾何在二維上的基本說明,請見射影平面。
雖然這些想法很早以前便已存在,但射影幾何的發展主要還是到19世紀才開始。大量的研究使得射影幾何變成那時幾何的代表學科。當使用複數的坐標(齊次坐標)時,即為研究復射影空間之理論。一些更抽象的數學(包括不變數理論、代數幾何義大利學派,以及菲利克斯·克萊因那導致古典群誕生的愛爾蘭根綱領)都建立在射影幾何之上。此一學科亦吸引了許多學者,在綜合幾何的旗幟之下。另一個從射影幾何之公理化研究誕生的領域為有限幾何。
射影幾何的領域又可細分成許多的研究領域,其中的兩個例子為射影代數幾何(研究射影簇)及射影微分幾何(研究射影變換的微分不變數)。
完全四邊形
完全四邊形是由任意四條直線組成的圖形,它們其中任意三條都不共點,且相交於六個點。如圖,直線AE、BE、AF、BI構成一個完全四邊形,直線AB、IF、EG為對角線。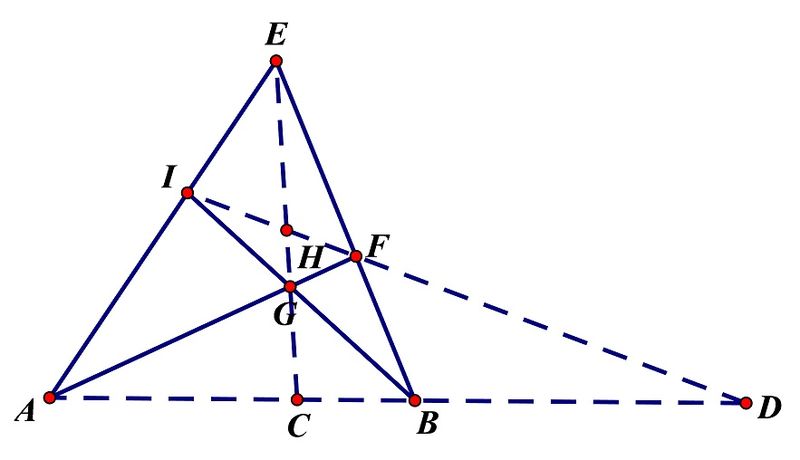 圖1
圖1
 圖1
圖1