極點是複函數裡面一種數學概念,在數理科學領域以及信息處理領域有及其廣泛的套用。
基本介紹
- 中文名:多重極點
- 外文名:Multiple pole point
- 分類:數理科學
- 套用領域:信息與通信
定義



相關性質
- 如果函式f的一階導數在a處具有簡單極點,則a是f的一個分支點,但反過來不成立。
- 一個既不是極點又不是分支點的非可去奇點稱為本性奇點。
- 除了一些孤立奇點外全純的函式,且所有的奇點均為極點,則該函式稱為亞純函式。
洛朗級數















極點是複函數裡面一種數學概念,在數理科學領域以及信息處理領域有及其廣泛的套用。



















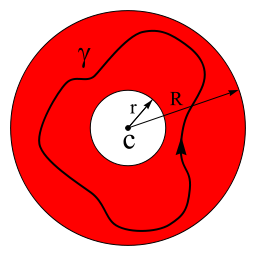
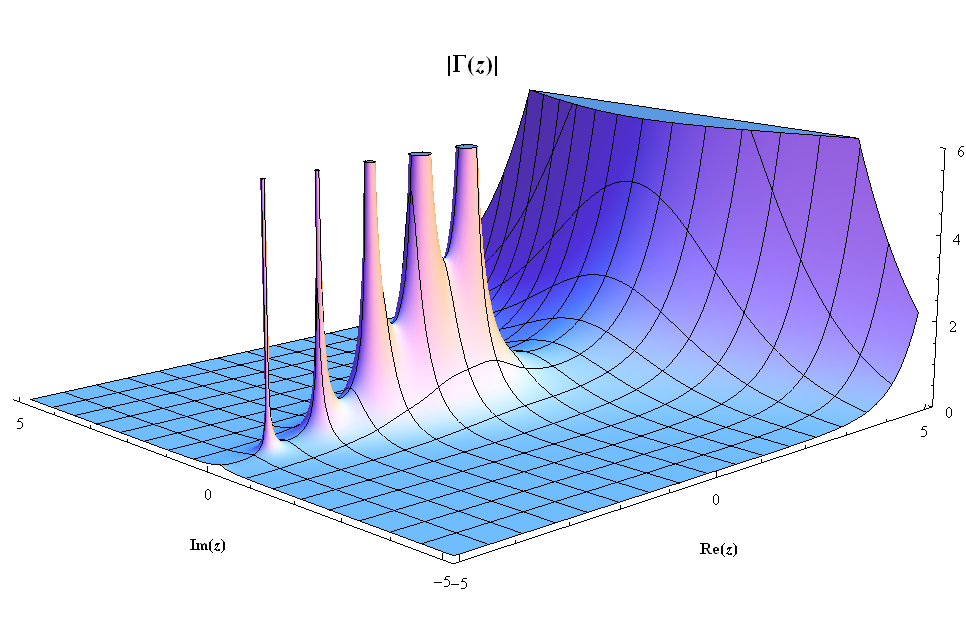
極點是複函數裡面一種數學概念,在數理科學領域以及信息處理領域有及其廣泛的套用。定義亞純函式的極點是一種特殊的奇點,它的表現如同 時 的奇點。這就是說,如果當z趨於a時,函式 趨於無窮大,那么 在z=a處便具有極點。假設U...
《多重隨機張量的極點性質及其在多作業問題中的套用》是依託河南師範大學,由崔魯賓擔任項目負責人的青年科學基金項目。項目摘要 多重隨機張量具有極其廣泛的套用背景。研究多重隨機集合的極點是研究多重隨機張量的重要途徑。本項目主要研究(m-1)-多重隨機張量集合的極點的等價性質、分類及求解極點的快速算法,其中m為...
2.3.2具有共軛複數極點的F(s)的部分分式展開式 2.3.3具有多重極點的F(s)的部分分式展開式 2.4拉普拉斯變換法的套用 第3章 控制系統的數學模型 3.1控制系統數學模型的建立 3.1.1概述 3.1.2線性控制系統數學模型的建立 3.2線性控制系統的傳遞函式 3.2.1傳遞函式的概念 3.2.2傳遞函式的幾點說明 3....
4.3.3 極點為多重極點 4.4 連續時間系統的復頻域分析 4.4.1 微分方程的拉普拉斯變換求解 4.4.2 電路網路的復頻域模型分析法 4.4.3 系統函式(轉移函式)4.5 系統特性與系統函式的關係 4.5.1 系統的因果性 4.5.2 系統的穩定性 4.5.3 由系統函式H(s)確定頻率回響 4.6 雙邊拉普拉斯...
11.2.1F(s)的極點均為單極點的情況 11.2.2F(s)有複數極點的情況 11.2.3F(s)有多重極點的情況 11.3動態電路的復頻域模型 11.3.1基爾霍夫定律的復頻域形式 11.3.2電阻元件的復頻域形式 11.3.3電感元件的復頻域形式 11.3.4電容元件的復頻域形式 11.3.5耦合電感的復頻域形式 11.3.6RLC元件串聯...
433極點為多重極點 44連續時間系統的復頻域分析 441微分方程的拉普拉斯變換求解 442電路網路的復頻域模型分析法 443系統函式(轉移函式)45系統特性與系統函式的關係 451系統的因果性 452系統的穩定性 453由系統函式H(s)確定頻率回響 46雙邊拉普拉斯變換 461...
研究了光纖中光孤子通訊技術方面起重要作用的帶修正項的非線性薛定鄂方程的解法,發現了一類新型的孤子解--多重極點孤子解。在繼續用這一處於場論層次上基本理論框架來處理問題的同時,近來我們對於量子色動力學Light-cone求和規則中的一種重要的非微擾客體即所謂light-cone光子波函式,開展了深入研究,這種研究對於研究...
2.5.2 只包含不同極點的F(s)的部分分式展開 2.5.3 包含多重極點的F(s)的部分分式展開 2.5.4 說明 2.6 用MATLAB進行部分分式展開 2.6.1 用MATLAB進行部分分式展開 2.6.2 用MATLAB求B(s)/A(s)的零點和極點 2.7 解線性定常微分方程 例題和解答 習題 第3章 動態系統的數學模型 3.1 引言 3....
A.3拉普拉斯變換定理 A.3.1實微分定理 A.3.2終值定理 A.3.3初值定理 A.3.4實積分定理 A.3.5復微分定理 A.3.6延時定理 A.3.7位移定理 A.3.8卷積定理 A.4拉普拉斯反變換 A.4.1概述 A.4.2部分分式展開 A.4.3含有多重極點的F(s)的部分分式展開 附錄B常用時間函式拉普拉斯變換 參考文獻 ...
控制前的系統其閉迴路極點在 及 。假設為了回響的考量,需讓閉迴路極點在 及 。理想特徵方程為 。依上述步驟,可得 ,而全狀態回授的系統特徵方程為 讓此特徵方程等於理想特徵方程,因此可得 因此,可以使閉迴路極點在理想位置上,讓回響也是理想值。此作法只在單一輸入的系統有效。多重輸入的系統也會有K矩陣,但...
