基本介紹
- 中文名:多元微積分
- 外文名:Multivariable calculus
- 又名:多變數微積分
- 本質:微積分學的一個組成部分
- 基於:微積分的基本思想的套用
- 套用學科:數學
歷史
多元函式
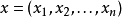
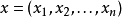
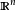
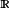
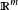
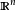
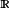
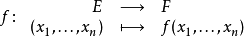
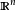
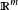
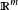
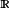
多元函式分析
極限與連續性
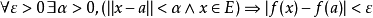
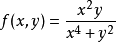
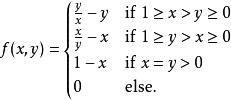
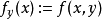
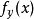
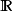
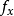
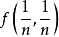
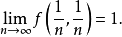
偏導數
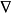
重積分
基本定理
- 梯度定理
- 斯托克斯定理
- 高斯散度定理
- 格林公式.
向量分析

多變數微積分一般指本詞條
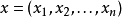
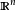
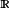
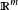
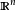
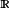
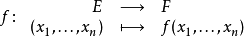
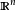
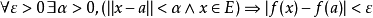
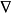
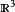
《分析基礎:微積分理論》作者為(美國)丁羅斯 (Ross.K.A),旨在為對嚴格的證明不熟悉的讀者,提供一本學習標準積分教程的後繼教程。對於學習高等分析教程,復變數、...
微分形式(differential form)是多變數微積分,微分拓撲和張量分析領域的一個數學概念。現代意義上的微分形式,及其以楔積和外微分結構形成外代數的想法,都是由著名法國...
#數學#Single Variable Calculus (單變數微積分)【字幕】Multivariable Calculus (多變數微積分)【字幕】Highlights of Calculus (微積分重點) 【字幕】...
1999秋季 多變數微積分課程,MIT2001春 本科生分析,麻省理工學院2001秋 本科生分析,麻省理工學院;多變數微積分課程,MIT2002春 主題關於辛拓撲,MIT2003...
第30章 多變數微積分II 第VII篇 附錄 附錄 索引[1] 參考資料 1. 經濟學中的數學 .豆瓣讀書[引用日期2012-12-20] 詞條標籤: 出版物 , 書籍 圖集...
是多變數多項式的一個著名問題,最初是由數學家Keller於1939年提出,之後Shreeram Abhyankar取現名,並將之廣為傳播,以作為代數幾何的問題中,只需稍多於微積分的知識...
《微積分重點》 全18集 翻譯至第18集《多變數微積分》全35集 翻譯至第35集《化學原理》全36集 翻譯至第31集《算法導論》 全6集 翻譯至第6集《計算機科學及...
《對於學習高等分析教程,復變數、微分方程、傅立葉分析、數值分析、多變數微積分以及統計的人來說讀《分析基礎:微積分理論》是很有必要的,也可以作為將來中學老師...
微分形式是多變數微積分,微分拓撲和張量分析領域的一個數學概念。現代意義上的微分形式,及其以楔積和外微分結構形成外代數的想法,都是由著名法國數學家埃里·卡當(...
書中講述了測地線、平行移動、曲率和凸性這些基礎知識,微分形式的介紹僅是為了在積分中的套用。這本教程需要有線性代數、多變數微積分和微分方程的預備知識,供中...
(0701M375) 多變數微積分(Multivariable Calculus) (0601H330) 日本史(History of Japan in East Asia) 15:30-17:30 (0105P110) 國際關係學(Introduction...
第十九章 含參變數積分第二十章 重積分第二十一章曲線積分與曲面積分第二十二章多變數微積分的基本定理·場論初步詞條標籤: 出版物 , 書籍 圖集 語言數學分析...
數學:代數、幾何、高等幾何、三角函式、函式、學前微積分、多變數微積分與線性代數、微積分、統計科學:生物、化學、套用化學、幾何物理、三角物理、高級物理、生物...
在以往的教學中,曾有學生問:在微積分中,講完單變數微積分,還要講多變數微積分,為什麼在複變函數課程中沒有多變數函式的理論?這是一個很自然的問題,但回答起來...
