基本介紹
- 中文名:多複變函數論
- 外文名:function theory of several complex variables
- 適用範圍:數理科學
簡介

研究方向
發展

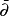




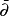

多複變函數論簡稱多復變。它是研究多個獨立復變數的全純函式性質的學科。就工具而言,由於多複變函數論中問題的複雜性,所以涉及拓撲、微分方程、微分幾何、代數...
數學中研究多個復變數的全純函式的性質和結構的分支學科,有時也稱多復分析。它雖然有著經典的單複變函數的淵源,但由於其特有的困難和複雜性,在研究的重點和方法...
《現代數學基礎:多複變函數論》包含多複變函數研究中分析、層論與復幾何這三個最主要方面的主要研究成果與方法。較之國內外相應的多複變函數著作,《現代數學基礎...
《華羅庚文集:多複變函數論卷1》是出版社於2010年出版的圖書,作者是華羅庚。 ...... 《華羅庚文集:多複變函數論卷1》包括這些論文的主要結果。在第一章中,證明...
華羅庚著,華羅庚以其專著《典型域上的多元複變函數論》獲得1956年度國家自然科學獎一等獎。...
複變函數論是數學中一個基本的分支學科,它的研究對象是復變數的函式。複變函數論歷史悠久,內容豐富,理論十分完美。它在數學許多分支、力學以及工程技術科學中有著...
《複分析導論:多複變函數》是2008年高等教育出版社出版的圖書,作者是沙巴特。本書主要介紹了多變數全純函式、基本的幾何概念、解析延拓、亞純函式和留數等知識。...
多復變數極大函式(Maximal function of several complex variables)是單位圓盤的極大函式在Bn中的推廣。...
多復變數內函式(inner function of severalcomplex variables)是單位圓盤的內函式在Bn中的推廣。由於單位圓盤上的內函式在單複變函數論中起著重要的作用,人們自然...
多復變數自守函式(automorphic function ofseveral complex variables)單復變數自守函式的推廣。...
多復變數亞純函式(meromorphic function ofseveral complex variables)是單復變數亞純函式的推廣。...
複變函數,是指以複數作為自變數和因變數的函式,而與之相關的理論就是複變函數論。解析函式是複變函數中一類具有解析性質的函式,複變函數論主要就是研究複數域上...
