三角形任一外角平分線外分對邊成兩線段,這兩條線段和夾相應的內角的兩邊成比例。
基本介紹
- 中文名:外角平分線定理
- 外文名:outer bisector theorem
- 所屬學科:幾何學
- 相關概念:三角形等角定理、正弦定理等
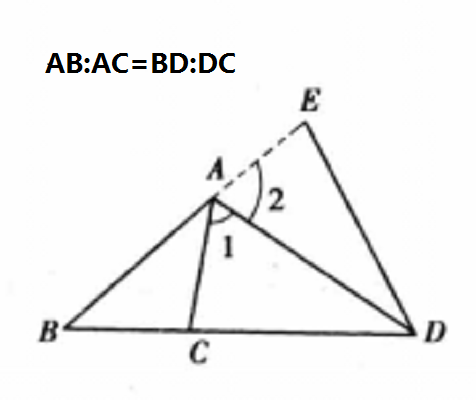
三角形任一外角平分線外分對邊成兩線段,這兩條線段和夾相應的內角的兩邊成比例。
三角形任一外角平分線外分對邊成兩線段,這兩條線段和夾相應的內角的兩邊成比例。...... 三角形外角平分線定理:三角形外角的平分線如果和對邊的延長線相交,它按...
角平分線定理1是描述角平分線上的點到角兩邊距離定量關係的定理,也可看作是角平分線的性質。角平分線定理2是將角平分線放到三角形中研究得出的線段等比例關係的...
拓展:在三角形中,已知其中兩個角的度數,根據三角形內角和定理,則能求出第三個角的度數。 [1] 三角形的外角平分線定理:三角形的外角平分線外分對邊所成的兩...
【角平分線逆定理】 1.到角兩邊的距離相等的點在角平分線所在直線或它外角平分線所在直線上。 2.平面內任意一小於180度的∠MAN如圖,直線BC分別交半直線AM、AN...
角平分線長公式描述了三角形內角平分線長與各線段間的定量關係。...... 由角平分線定理得即代入①中得證畢。...在△ABC中,∠A的外角平分線記為 ,∠B的...
三角形內外角平分線定理三角形ABC內角A的平分線交線段BC於H,則AB:AC=BH:HC。三角形ABC的角A的外角的平分線與線段CB的延長線交於H,則AB:AC=BH:HC。...
第二節三角形內角與外角平分線定理 第三節射影定理 第四節三角形的重心、垂心、外心、內心 5.4.1三角形的重心 5.4.2三角形的垂心 5.4.3三角形的外心...
過P點作角APB的內、外角平分線,交AB與AB的延長線於C,D兩點由角平分線性質,...與切割線定理相似 兩條割線交於p點,割線m交圓於A1 B1兩點,割線n交圓於A2 ...
4.1.2 三角形內角與外角平分線定理4.1.3 相似三角形與射影定理4.2 三角形的重心、垂心、內心、外心4.2.1 三角形的重心4.2.2 三角形的垂心...
