基本介紹
- 中文名:外公切線
- 外文名:external common tangent
- 所屬學科:數學(幾何學)
- 相關概念:相切,切線,兩圓相切等
- 特點:兩圓在公切線的同旁
兩圓切線
 圖1
圖1

作兩個圓切線
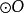
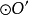
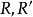
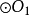
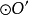
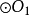
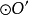
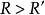
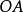



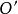

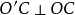
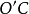
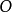
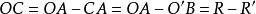
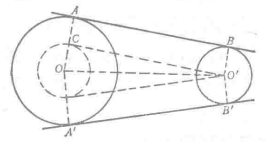 圖2
圖2


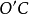



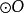
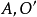





 圖1
圖1

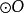
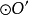
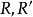
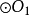
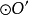
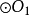
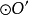
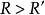
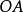



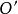

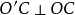
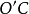
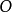
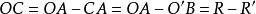
 圖2
圖2


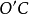



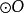
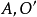




如果一條直線和兩個圓都相切,這條直線叫做兩個圓的公切線。如果兩圓在公切線的同側,稱這條公切線為兩圓的外公切線,如果兩圓分別在公切線的兩側,稱這條公...
公切線是指同時相切於兩條或兩條以上的曲線的直線,例如和兩個圓相切的直線叫做這兩個圓的公切線。如果兩個圓在公切線的同側,則這公切線叫外公切線;如果兩個...
如果一條直線和兩個圓都相切,這條直線叫做兩個圓的公切線。如果兩圓在公切線的同側,稱這條公切線為兩圓的外公切線,如果兩圓分別在公切線的兩側,稱這條公...
特別地,兩個不重合的圓總是位似的,位似中心為兩圓外公切線或內公切線的交點。位似性質 編輯 位似是特殊的相似。位似圖形對應邊平行,對應點的連線交於一點,這一...
如果兩圓不相交,可選直線為兩圓的兩條外公切線加兩條內公切線。 直線延長 選定直線 = 交於線,圓,弧 延長直線直至於另一選定直線、圓或圓弧相交。 有兩...
如果將圓 的外公切線的長度設為 ,那么開世定理聲稱,有下列等式成立。 [1] 可以注意到,如果四個內切的圓都退化成點的話,就會變成圓 上的四個點,而開世定理...
內還是在圓 外), 是外部公切線的長度;(2)如果 從不同的側面切線, 是內部公切線的長度。凱西定理的放過來也成立,即,如果等式成立,則圓圈與公共圓相切。參考...
當兩圓內切時,過D作兩圓外公切線上與B同側一點為E,與C同側一點為F聯結DP,DQ並延長,交外接圓於S,T.聯結BD,AD,PQ,SA.因為∠PDE=∠PQD=∠BPD=∠BAD+...
146內公切線長= d-(R-r)外公切線長= d-(R+r) (還有一些,大家幫補充吧)國中公式常用公式 編輯 常用數學公式:[1] 乘法與因式分 a2-b2=(a+b)(a-b)...
除上述特性外,隨同膨脹變換的還有圓的切線隨著變換而進退,其進退的距離恰等於所選的膨脹參數,這些事理對作圖特別有用在中學課本上,關於兩圓公切線的作圖就是套用...
38. 與外公切線平行 39. 更一般些 40. 姜霽恆的問題 41. 共同的點 42. 三個圓三 非常規的幾何問題 43. 整數知識 44. 條件夠嗎? 45. 滾動的圓(一) ...
中位線 相似形 比例尺 內分點 外分點 平面圖 同心圓內切圓 外接圓 弦心距 圓心角 圓周角 弓形角 內對角連心線 公切線 公共弦 中心角 圓周長 圓面積 反證...
有時為了省去一個純剪應力狀態(薄壁圓管扭轉)破壞試驗,也可以用圓I和圓II的外公切線近似地代替包絡曲線段。為了考查上述各種強度理論的適用範圍,自17世紀 以來,...
在歐氏幾何學中,將一個命題中的某些點換成圓,將這些點中某兩點的連線換成兩圓的公切線,將兩點間的距離換成兩圓的公切線(或連心線)的長,將另一點和這些點...
