曼海姆定理

曼海姆定理是指有一圓分別與三角形ABC的外接圓⊙O和直線AB,AC相切於D,P,Q，則PQ中點為三角形ABC的內心或旁心。

若它與外接圓內切，即為內心；外切即為旁心。

基本介紹

• 中文名：曼海姆定理
• 外文名：Mannheim theorem
• 提出者：曼海姆
• 套用學科：數學
• 適用領域範圍：幾何學

內容

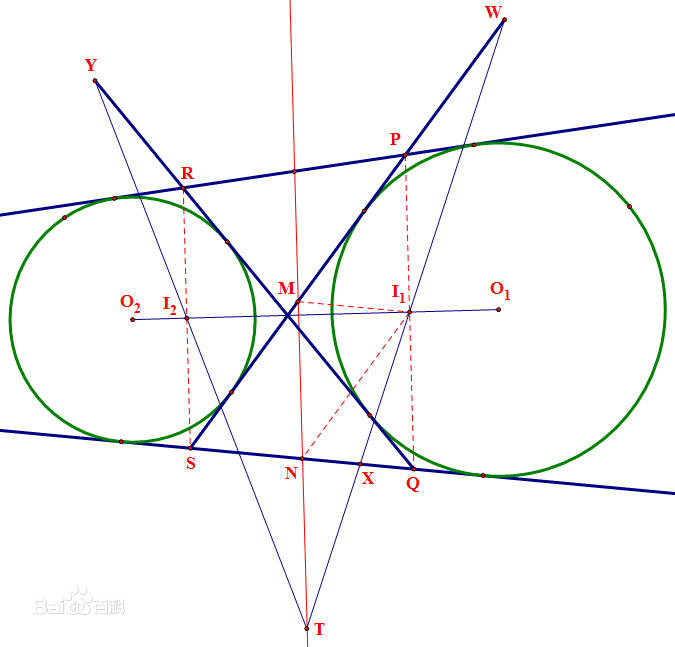
1、 在三角形ABC的外接圓⊙O中，另有一圓⊙M分別與其內切，並和AB,AC相切於D,P,Q，則PQ中點為三角形ABC的內心。

2、 在三角形ABC的外接圓⊙O外，另有一圓⊙M分別與其外切，並和AB,AC延長線相切於D,P,Q，則PQ中點為三角形ABC的旁心。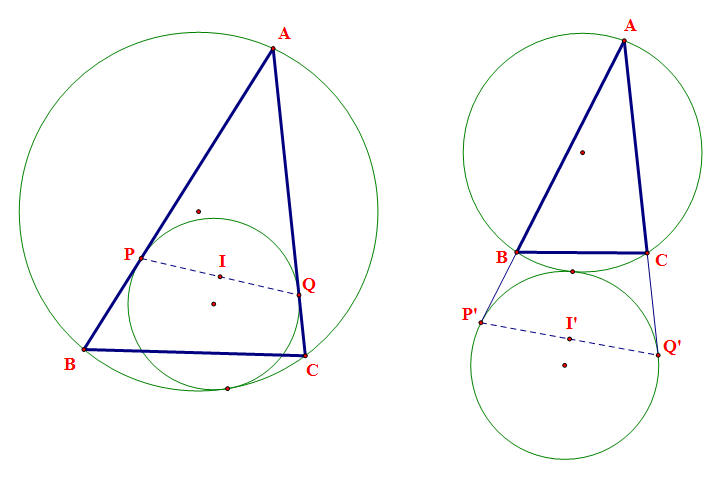

證明

當兩圓內切時,過D作兩圓外公切線上與B同側一點為E，與C同側一點為F

聯結DP,DQ並延長，交外接圓於S,T.聯結BD,AD,PQ,SA.

因為∠PDE=∠PQD=∠BPD=∠BAD+∠ADS,

∠SDE=∠SAD=∠SAB+∠BAD,

所以∠ADS=∠SAB，

所以S為弧AB中點,

所以S.I.C共線.

同理，B.I.T共線.

連線SC,BT.

對ABTDSC運用Pascal定理，則P.I.Q共線.

易知PQ⊥AI，故PI=IQ，I為PQ中點.

命題得證。

當兩圓外切時，類似可證。