地圖著色(map coloring)是一種組合構形，它是對於地圖面集的一種分劃，分配地圖的每一個面一種顏色，使得相鄰的面(指有公共邊界邊)具有不同的顏色，稱這樣一種色的分配為這個地圖的一個著色，或者說，將地圖的面集分劃為若干個子集，使得每個子集中的任何兩面均不相鄰，這樣就可以將每個子集中的面用一種顏色著染使得不同子集用的顏色不同，在地圖M的所有著色中，使用顏色最少的著色的顏色數目稱為地圖M的色數，地圖的頂點著色，或者說，對於與它同構的圖的頂點做正常著色，就是其對偶地圖的地圖著色。
基本介紹
- 中文名：地圖著色
- 外文名：map coloring
- 所屬學科：數學
- 所屬問題：組合學(圖與超圖)
- 簡介：對於地圖面集的一種分劃
基本介紹,相關分析,
基本介紹
地圖著色是指分配地圖的每一個面一種顏色，使得相鄰的面(指有公共邊界邊)具有不同的顏色。
將一個平面圖的區域設為頂點，如果兩個區域有公共邊，用邊連線這兩個區域所轉換的頂點，這樣得到的圖稱為原平面圖的對偶圖。
圖a的對偶圖為圖b。
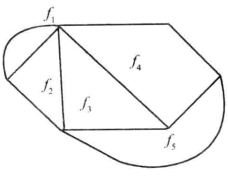
圖a
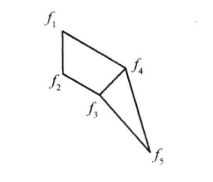
圖b
定理1 平面圖的對偶圖必是平面圖。
定理2（地圖著色的五色定理） 任何一個平面地圖都可用至多5種顏色著色。
證 給平面圖中各區域著色就相當於給這個平面圖的對偶圖的各頂點著色。根據五色定理，任意一個平面圖都至多可用5種顏色著色，所以，給任意一個平面圖的所有區域著色也至多可用5種顏色。這樣就得到下面的定理。
定理3（地圖著色的四色定理） 任何一個平面地圖都可用至多4種顏色著色。
相關分析
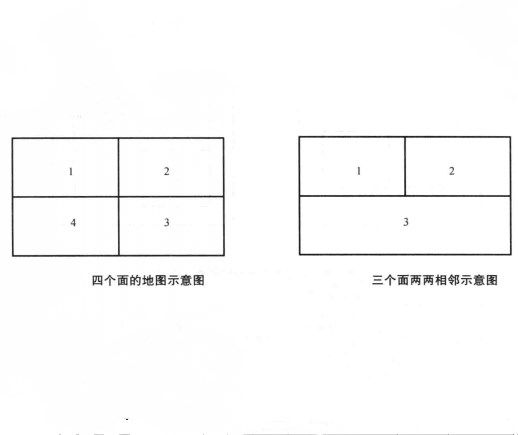
地圖是由網路劃分的一些區域所構成的圖形，所謂地圖著色，就是給地圖的每個區域塗上一種顏色，使得相鄰的兩個區域塗有不同的顏色。這裡規定，每個區域必須由一個單連通域構成，而兩個區域相鄰是指它們具有一段公共的邊界線(而不僅只有一個公共點)。如圖1中所示，區域1與3，2與4不能算為相鄰，區域1與2，2與3，3與4，1與4才能稱為相鄰的區域。
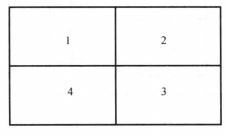
圖1四個面的地圖示意圖
圖2 三個面兩兩相鄰示意圖
地圖著色問題是指：最少需要幾種顏色能夠完成地圖著色。著名的四色猜想為：在一個平面或球面上的任何地圖能夠只用四種顏色來著色。
為了理解四色猜想問題，我們不妨先分析一下平面或球面上能夠組成一組相鄰(即兩兩相鄰)的區域數最多是幾個。
先來看平面地圖，我們先從最少的數目開始排列。兩個區域相鄰是任何人都知道的；三個區域，要每兩個互相相鄰，可由圖2表示。若是四個區域組成一組相鄰區域能行嗎?由圖3所示，可以做到。
顯然，若是再加上一個區域——第五區域，就不能同時與1，2，3，4區域都相鄰，因此，五個區域不能組成一組兩兩相鄰的區域組。也就是說平面上能構成兩兩相鄰的區域組裡區域最多有四個。
在球面上，構成區域組的區域不會多於四個，這與平面上的情形一樣。可是區域分布情形比平面上更單純，因為在球面上沒有圍繞與被圍繞的區別。例如從人類的立場來說，陸地被海洋圍繞，可是從魚類的立場來看，海洋卻是被陸地所圍繞。注意，球面上不允許出現環帶狀的區域，否則球面將分為上下兩個不相鄰的部分，這不是我們要考慮的情況。因此球面上四個區域組成一組相鄰區域，分布如圖4(a)所示，區域1以CD，DA，AC為界分別與區域2，3，4相鄰，區域2以BD，BC為界與區域3，4相鄰，區域3與4以AB為界而相鄰，這樣一來球面上區域相鄰的情形就確定了。圖4(b)所示的四面體，四面體的四個面的分布與球面上四個區域組成一組相鄰區域的情形是一樣。因此，要討論球面上區域相鄰情況只要討論四面體就行了。
從以上分析的結果看出，平面上或者球面上能夠構成相鄰情形的區域最多數目都是四個。從這一點來看，地圖著色用四種不同顏色足以區別不同的區域。但這種直觀的認識是不夠用來證明這一著名猜想的。
關於四色猜想問題，一個多世紀以來吸引著許多的學者與專家，普遍的看法是認為猜想是正確的，但是未必可以普諞帥l證明。1976年9月，美國伊利諾斯大學的阿貝爾(K.Appel)和哈肯(W.Hakan)宣布：在計算機的協助下證明了四色猜想。對四色同題的研究，推動了數學的發展，產生了一些新的數學理論和數學計算技巧。
