在有限二人零和對策中,稱存在鞍點的對策為嚴格決定了的對策(稱矩陣遊戲更妥當),簡稱嚴格決定對策(strictly determined game),有些對策沒有鞍點,有些則有許多鞍點。
基本介紹
- 中文名:嚴格決定對策
- 外文名:strictly determined game
- 所屬學科:數學
- 所屬問題:運籌學
- 相關概念:二人零和對策
基本介紹
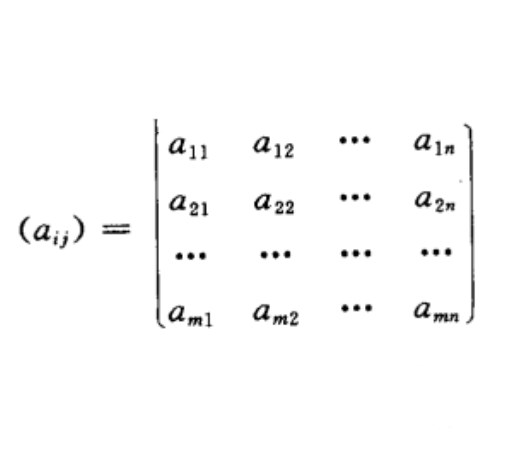
B | |||||
A | 1 | 2 |  | n | |
1 |  |  |  |  | |
2 |  |  |  |  | |
 |  |  |  | ||
m |  |  |  |  | |








兩人零和對策與嚴格決定對策












在有限二人零和對策中,稱存在鞍點的對策為嚴格決定了的對策(稱矩陣遊戲更妥當),簡稱嚴格決定對策(strictly determined game),有些對策沒有鞍點,有些則有許多鞍點。
B | |||||
A | 1 | 2 |  | n | |
1 |  |  |  |  | |
2 |  |  |  |  | |
 |  |  |  | ||
m |  |  |  |  | |




















在有限二人零和對策中,稱存在鞍點的對策為嚴格決定了的對策(稱矩陣遊戲更妥當),簡稱嚴格決定對策(strictly determined game),有些對策沒有鞍點,有些則有許多鞍點。...
它是在多級遞階決策系統中,由於決策人所處的地位不同,所形成的一種新的對策形式。由經濟學家斯塔克爾貝格提出。社會現象的結局通常是由許多決策人的行動共同決定的...
2016年11月16日,中共四川省委十屆九次全會通過《中共四川省委關於加強和規範黨內政治生活嚴格黨內監督鞏固發展良好政治生態的決定》。該《決定》分牢固樹立“四個意識...
最高人民檢察院關於嚴格執行全國人大常委會《關於嚴禁賣淫嫖娼的決定》和《關於嚴懲拐賣、綁架婦女、兒童的犯罪分子的決定》的通知在1991.09.17由最高人民檢察院頒布...
美國瀕危物種保護法律對策程式 首先,對瀕危物種或受威脅物種保護範圍的增減及物種生境的決定,由相關的利害關係人(interested person)提出申請,在收到申請後的90天內...
《關於切實加強信貸管理嚴格控制貨幣發行的決定》(此後簡稱“《決定》)由國務院於1981年1月29日發出,《決定》提出了八項要求,給予了管理控制監管的規範。《決定》接...
2004年10月21日,國務院下發了《國務院關於深化改革嚴格土地管理的決定》(國發〔2004〕28號),這是近年來國務院出台的關於土地管理的最全面、最明確、規格最高的一...
《國務院關於進一步加強環境保護工作的決定》由國務院於1990年12月5日以國發〔1990〕65號發布,包括嚴格執行環境保護法律法規、依法採取有效措施防治工業污染等八部分...
《最高人民法院關於必須嚴格控制對被執行人採取拘捕措施的通知》在1996.10.09由...四、高級人民法院批准逮捕後,受案法院應當製作逮捕決定書,交由同級公安機關執行...
7個調研組,赴各地開展了安全培訓工作專題調研,專題研究加強安全培訓工作的對策...《決定》是國務院安委會第一次以“決定”的形式發布的規範性檔案,也是學習貫徹...
四、各級人民檢察院在貫徹執行《決定》中,要加強調查研究,不斷積累和總結經驗,注意研究《決定》規定的各種犯罪的特點、規律及其對策;對在執行《決定》中遇到的問題...
《中共四川省委關於加強和規範黨內政治生活嚴格黨內監督鞏固發展良好政治生態的決定...其是、各自為政,決不允許有令不行、有禁不止,決不允許上有政策、下有對策...
2014年2月28日,陝西省人民政府印發《關於加強環境保護推進美麗陝西建設的決定》...(PM10)、二氧化硫、氮氧化物、揮發性有機物污染控制,加強技術研究與管理對策研究...
《關於檢察機關反貪污賄賂工作若干問題的決定》,該《決定》的基本精神和有關規定...要樹立強制措施是保障刑事訴訟順利進行的法定手段,是法律規定的重要偵查對策的觀念...
實行最嚴格的耕地保護制度,這是由我國人多地少的基本國情決定的,是由農業的基礎地位決定的,更是由土地對於維護社會長治久安的重要性決定的。我們必須進一步提高...
