基本介紹
- 中文名：單峰映象
- 外文名：logistic map
- 方式：簡單非線性動力方程
- 發起：生物學家Robert May
- 時間：1976年
緒論,r的值對結果的影響,單峰映象和混沌,相關條目,
緒論
單峰映象（logistic map）是種二次的多項式映射（遞推關係式），是一個由簡單非線性方程產生混沌現象的經典範例。這種映射因生物學家Robert May在1976年發表的一篇論文而著名。單峰映象原本被Pierre François Verhulst用作一個人口學模型，後來套用在物種受到限制因素之下的數目。數學上可寫成
其中
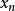
r是正整數，是根據繁殖和餓死率而得出的數。
單峰映象是根據以下兩個現象：
- 當人口少時，繁殖增加的人口大致跟物種的原本總數目成正比；
- 環境資源有一“最大容量”，當人口接近最大容量時，人口可能會下降。
可是在特定初始條件及參數時，單峰映象的人口模型會出現負的人口數，較早期使用的Ricker模型也有混沌現象，但沒有這種問題。
r=4的單峰映象是位元移動映射及參數μ=2的帳篷映射的非線性變換。
r的值對結果的影響
變化參數r的值，其結果如下：
0和1之間：不論啟始值數值為何，xn會越來越少，最後趨近於0。
1和2之間：不論啟始值數值為何，xn會快速的趨近
。
2和3之間：經過幾次疊代，xn也會越來越接近
，但一開始會在這個值左右振動，而收斂速率是線性的。
3：xn仍然會越來越接近
，但收斂速率極為緩慢，不是線性的。
3和
（約3.45）之間：針對幾乎所有的初值，xn最後會在2個值之間持續的震盪，即 xn最後會是a,b,a,b...的變化，其數值和r有關。
3.45和大約3.54之間，針對幾乎所有的初值，xn最後會在4個值之間持續的震盪。
約大於3.54： xn最後會在8個、16個、32個值……之間持續的震盪，至於r何時會令xn的值由n個到2n個，則和費根鮑姆常數有關。
約為3.5699：這樣的振動消失，整個系統開始在混沌的狀態之中。針對幾乎所有的初值，都不會出現固定周期的震盪，初值再微小的變化，隨著時間都會使結果產生明顯的差異，這就是典型混沌的特性。
大於3.5699：整個系統在混沌的狀態之中。不過，當中有些特定的r值還是使系統變成非混沌，有周期性的結果，這些區間稱為“穩定島”。例如當r約大於3.82，會出現3個值的周期，再大一點出現6個值及12個值的周期。
當r從大約3.5699到大約3.8284之間，系統混沌性質發展的現象有時會稱為Pomeau–Manneville場景，其特徵是周期性的震盪和非周期性的行為會穿插出現。此特徵可以套用在半導體元件中。也有其他區域會使系統的周期為5個值，不管任意周期都存在某特定的r，使周期為指定值。
大於4：針對幾乎所有的初值，系統最後都會超過區間[0,1]並且發散。
對於任一個r值，最多只有一個穩定的極限環，若穩定極限環存在，幾乎所有的點最後都會趨近極限。若某一個r值有一個穩定的極限環，可能也有無限個不同周期的不穩定極限。
這些情況可用分枝圖表示，分枝圖中的橫軸是參數r的數值，縱軸中顯示大部分初值下，穩態可能的x值，若最後數值會在2個值中震盪，分枝圖上對應的數值就會有2點。若某特定r值下，已無法明確的看到有幾個對應的點，當時系統可能已經在混沌狀態下。
分枝圖有自相似的特性。若將分枝圖中 r=3.82的部分展開，只取三個分支中的一個。其圖形會好像是原分枝圖縮放及扭曲後的結果。針對所有非混沌的參數r都有此一特性。以此可以看出混沌和分形深入及明顯的關係。
單峰映象和混沌
和其他混沌系統比較，單峰映象較為簡單，是一個說明混沌特性的很好的例子。簡單來說，混沌就是對初始條件的高度靈敏度。r是在3.57及4之間的大部分數值都可以使單峰映象出現此一特性。對初始條件有高度靈敏度的常見原因是映射本身是對定義域的拉伸及摺疊。單峰映象的二次差分方程可視為是對於區間(0,1)拉伸及摺疊的過程。
利用二維及三維的相圖可以看出一些單峰映象的特性。以r=4的單峰映象為例，二維相圖為一拋物線，但是若用
繪製三維相圖，可看出進一步的結構，例如幾個一開始很接近的點在疊代後開始發散．特別是位在斜率較大位置的點。
拉伸及摺疊的結果使疊代的數列以指數形式發散（參照李亞普諾夫指數），可以用有混沌特性時，單峰映象的複雜及不可預測性說明這一點。事實上，數列的指數發散說明了混沌和不可預測性之間的關係：初值微小的誤差在疊代過程中會以指數成長的方式增加。因此當對於初始狀態的資訊中有微小的誤差時．對未來狀態的預測準確度也會隨疊代次數增加而快速變差。
由於映象是限制在實數數線的一段範圍內，其維度小於或等於1。依數值分析的結果，在r=3.5699456...時（剛開始混沌特性時），其關聯維度為0.500 ± 0.005（Peter Grassberger,1983）、豪斯多夫維數大約是0.538，而分形維數為0.5170976...。
有些混沌系統可對於其未來狀態的可能性作準確的描述。若一個可能有混沌特性的動態系統存在吸引子，則存在一機率量測描述系統長期下，在吸引子各部分所花時間的比例。以r=4的單峰映象而言，啟始狀態在區間(0,1)中，而吸引子也在間(0,1)中，其機率量測對應參數a=0.5,b=0.5的Β分布，其不變測度為
。不可預期性和隨機不同，不過在一些情形下這二很類似，而且即使對單峰映象（或其他混沌系統）初值只有很少的資訊，仍然可以針對長期的分布作某種程度的預測。
相關條目
- 剛性方程
