基本介紹
- 中文名:單位矢量
- 外文名:unit vector
- 套用領域:物理學
- 特點:有大小有方向且模為一
單位矢量的引入
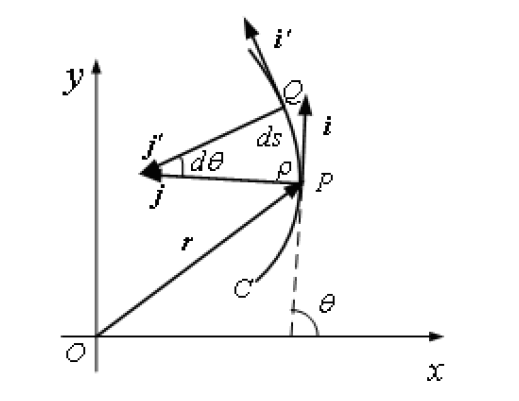 圖一 自然坐標系單位矢量的含義圖 質
圖一 自然坐標系單位矢量的含義圖 質





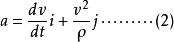

自然坐標系單位矢量的新認識



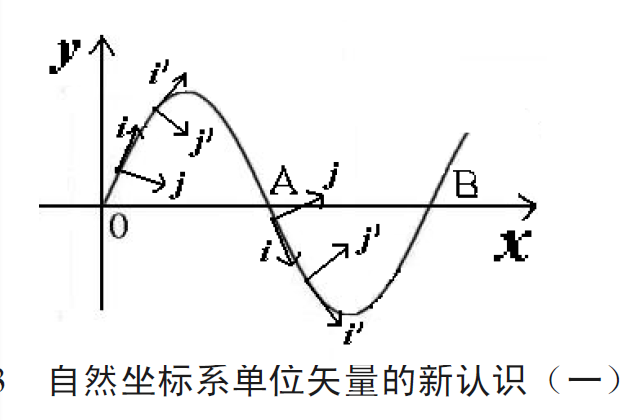 圖二 自然坐標系單位矢量的新認識(一)
圖二 自然坐標系單位矢量的新認識(一)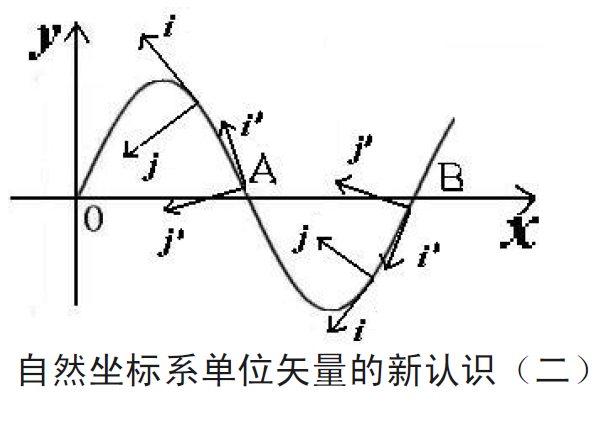 圖三 自然坐標系單位矢量的新認識(二)
圖三 自然坐標系單位矢量的新認識(二)
單位矢量正向的選取
自然坐標系

選取方法








 圖一 自然坐標系單位矢量的含義圖 質
圖一 自然坐標系單位矢量的含義圖 質









 圖二 自然坐標系單位矢量的新認識(一)
圖二 自然坐標系單位矢量的新認識(一) 圖三 自然坐標系單位矢量的新認識(二)
圖三 自然坐標系單位矢量的新認識(二)








單位向量是指模等於1的向量。由於是非零向量,單位向量具有確定的方向。單位向量有無數個。一個非零向量除以它的模,可得所需單位向量。一個單位向量的平面直角坐標...
既有大小又有方向的物理量叫做矢量,而大小為一個單位的矢量就是單位矢量。例如位移、速度、加速度、力、力矩、動量、衝量等,都是矢量。自然坐標系中的單位矢量如...
矢量運算,矢量之間的運算要遵循特殊的法則。矢量加法一般可用平行四邊形法則。由平行四邊形法則可推廣至三角形法則、多邊形法則或正交分解法等。矢量減法是矢量加法的...
平面向量是在二維平面內既有方向(direction)又有大小(magnitude)的量,物理學中也稱作矢量,與之相對的是只有大小、沒有方向的數量(標量)。平面向量用a,b,c上面...
矢量(vector)是一種既有大小又有方向的量,又稱為向量。一般來說,在物理學中稱作矢量,例如速度、加速度、力等等就是這樣的量。捨棄實際含義,就抽象為數學中的...
矢量圖像,又稱為向量,也稱為面向對象的圖像或繪圖圖像,在數學上定義為一系列由線連線的點。在遊戲開發中,向量還有類似於物理方面釋義的含義。設對象a,我們可以...
取左矢量(或右矢量)的一個集合,使任意左矢量(或右矢量)都能表示為它們的線性組合。這些左矢量(或右矢量)稱為表象的基左矢(或基右矢)。基左矢和基右矢總稱...
伯格斯矢量(Burgers vector)是伯格斯提出了用晶體的滑移矢量表示位錯引起的晶體畸變的方法。...
所有的列向量的集合形成一個向量空間,它是所有行向量集合的對偶空間。 單位列向量,即向量的長度為1,其向量所有元素的平方和為1。...
*運算結果c是一個偽向量。這是因為在不同的坐標系中c可能不同。 [1] 向量積坐標運算 設=(),=()。i,j,k分別是X,Y,Z軸方向的單位向量,則 [1] :...
然後,有一些坐標變換,首先通過3/2變換,變成旋轉的d-q坐標,然後通過前面的磁鏈方程產生的單位矢量來得到旋轉坐標下的類似於直流機的轉矩電流分量和磁場電流分量,這樣...
向量加法的單位元:V 里有一個叫做零向量的 0,∀ v ∈ V , v + 0 = v; 向量加法的逆元素:∀v∈V, ∃w∈V,使得 v + w = 0; 標量乘法分...
單位位錯,也稱特徵位錯,就是指它的柏氏矢量等於晶體中最短的點陣矢量的位錯。...... 單位位錯,也稱特徵位錯,就是指它的柏氏矢量等於晶體中最短的點陣矢量的位...
距離矢量(Distance Vector)是兩個路由算法中的一個。另一類是鏈路狀態路由選擇。基本上,路由協定基於距離矢量算法根據目的地的遠近來決定最好的路徑,鏈路狀態協定是...
三個相互正交的矢量構成的三維空間。...... 基矢量:構成矢量基的三個單位矢量 e1,e2,e3V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:1次歷史版本 最近更新: ...
特徵向量求特徵向量 一旦找到特徵值λ,相應的特徵向量可以通過求解特徵方程(A –λI) v = 0 得到,其中v為待求特徵向量,I為單位陣。...
所謂矢量,就是有方向又有大小的量,顧名思義,矢量噴口就是可以改變噴射方向的噴口,通過改變噴口方向來產生不同方向的加速度,矢量噴口技術對戰鬥機的隱身、減阻,...
一個矢量,它的方向表示電磁波的等相位面行進的方向。波矢是波的矢量表示方法。波矢是一個矢量,其大小表示波數,其方向表示波傳播的方向。...
偽矢量又稱贗矢量,即兩個向量的叉積就稱為偽向量,一般的矢量(極矢量)在坐標系反演時會改變方向,而偽矢量(軸矢量)不會改變方向,有關偽矢量的例子還有角速度,...
矢量數據主要是指城市大比例尺地形圖。此系統中圖層主要分為底圖層、道路層、單位層,合理的分層便於進行疊加分析、圖形的無逢拼接以實現系統圖形的大範圍漫遊。矢量...
矢量網路拓撲圖是指用傳輸媒體互連各種設備的物理布局。將參與LAN工作的各種設備用媒 體互連在一起有多種方法,實際上只有幾種方式能適合LAN的工作。 矢量網路拓撲...
物理量單位通過物理定律及其方程建立相互間的關係。它們中有的有方向,有的無方向;有的有量綱(見量綱分析)、單位 ,有的無量綱、單位;有的描述狀態,有的描述過程;...
