基本介紹
- 中文名:商映射
- 外文名:quotient mapping
- 所屬學科:數學
- 性質:一種連續映射
定義




相關定理

























常用命題






舉例















































商映射(quotient mapping),是一類連續映射。設R為集合E中的等價關係,f為從E到集合F中的與R相容的映射。從E/R到F中使x的類對應f(x)的映射g叫做通過對R求商從f導出的映射。設S為F中的等價關係,如...
在泛函分析中,開映射是一類特殊的映射。如果巴拿赫空間之間的連續函式是滿射的,那么它就是一個開映射(open mapping)。如果X和Y是巴拿赫空間,A: X → Y是一個滿射的連續線性運算元,那么A就是一個開映射(也就是說,如果U是X內的...
因此,大多數的研究中,採用啟發式算法來求解虛擬網路的最佳化映射問題。現有的啟發式解決方案可以分為兩大類:離線VN映射問題解決方案 線上VN映射問題解決方案。在離線問題中,所有業務提供商的VN請求是事先己知的。致力於底層物理網路負載...
對於使用靜態IP接入的用戶而言,特別是使用獨立主機託管的用戶,您可以利用nat123連線埠映射提供的域名映射服務來避免在不斷轉換服務商時,需要不斷向域名解析服務商重複複雜的修改IP指向過程,完全實現域名解析指向的自主性。功能介紹 nat123是...
但是,它並不是集合意義下的映射。代數簇是代數幾何的基本研究對象。設k是一個域,域k上的代數簇就是一個整的、分離、有限型k概形。這裡的基域k往往被取作代數閉域。有理函式是指由有理式表示的函式,即兩個多項式函式的商(分母...
機房、防火牆許可權的網路進行連線埠映射、中轉,同時支持多連線埠映射!運行平台:Win( 2K/ XP/ 03/ Vista/ 7/ 2008) 開發商: ZNZNET 功能簡介:區域網路映射、區域網路中轉、遠程類軟體上線、驗證,區域網路USB軟體共享連線、區域網路架設FTP、WEB。
本書介紹了近幾年關於三角代數及其相關代數上映射問題的研究成果。前9章介紹了多重交換化映射、強交換保持廣義導子、Lie多重導子、雙導子、Lie同構、Jordan滿同態等結果。後3章介紹了函式恆等式和極大左商環在三角環上的套用。具有...
ENUM是電話號碼映射(E.164 Number URI Mapping)的縮寫。這個縮寫的後面隱藏著一個偉大的創意:即通過最好和最廉價的路由途徑,可以在世界任何地點使用同一個電話號碼。您可以象註冊域名一樣註冊ENUM號碼。有許多註冊機構和VOIP服務商免費...
NAT連線埠映射協定(英語:NAT Port Mapping Protocol,縮寫NAT-PMP)是一個能自動創建網路地址轉換(NAT)設定和連線埠映射配置而無需用戶介入的網路協定。簡介 該協定能自動測定NAT網關的外部IPv4地址,並為應用程式提供與對等端交流通信的方法...
《對應役滿DS》 是日本遊戲製造商Nintendo公司製作的一款遊戲。遊戲包括“麻將入門”、“危險牌預測”、“麻將詞典”等模式在。遊戲內容 《對應役滿DS》 是日本0遊戲製造商Nintendo公司製作的一款遊戲。遊戲包括“麻將入門”、“危險牌預測...
《全球映射:我真不是大反派》是一本都市小說,作者是風唐大大。內容簡介 遊戲映射現實,其他人都是繼承玩家修為。只有徐青不僅繼承了玩家修為,還化身成了讓全世界陷入恐慌的終極大BOSS。為了證明自己不是大反派,於是徐青開始用大boss的...
轉化為K上一個向量空間,成為零類。相對應的,商映射即定義為 與等價類 之映射 性質 (1)反身性:(2)對稱性: 若 則 (3)傳遞性: 若 則 拓撲空間 定義 設X為拓撲空間,~為X的等價關係。π:X→X/~為典範映射...
商空間首先出現在穆爾(Moore,R.L.)於1925年發表的論文和亞歷山德羅夫(Александров,П.С.)於1927年發表的論文中,兩位作者僅討論了特殊情形,即由上半連續分解確定的商空間.商空間的一般概念及商映射的概念是由比爾(...
商範疇(quotient category)是代數系的商代數系及局部化的高度推廣。範疇是範疇論的基本概念之一。商代數是一個代數結構模它的同餘關係產生的新的代數結構。一個代數結構必定與它的商代數同態,把任一元素對應到這個元素所在的等價類的映...
具體內容有下面這些方面的習題:拓撲空間的基本概念,連續映射,拓撲基與積空間,分離性公理與可數性公理,引理及其套用,緊緻性與列緊性,局部緊性與仿緊性,連通性,道路連通性,商映射與商空間,幾個典型曲面與閉曲面分類定理,點網與...
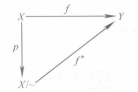
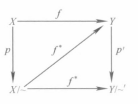
φX, φY 是分別商映射與到X 和 Y 不交並的典範單射的複合。可以將 i 換成任意一個連續映射 g 構造一個一般的推出——過程是類似的。反之,如果 f 也是一個包含黏著構造不過是將 X 與 Y 沿著它們的公共子空間簡單的黏合。
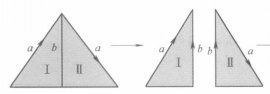
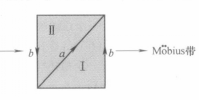
第三章 商空間與閉曲面 1 幾個常見曲面 2 商空間與商映射 3 拓撲流形與閉曲面 4 閉曲面分類定理 第四章 同倫與基本群 1 映射的同倫 2 基本群的定義 3 Sn的基本群 4 基本群的同倫不變性 5 基本群的計算與套用 6 Jordn曲線...
區域網路通是專業的區域網路連線埠映射軟體,可輕鬆訪問連線區域網路,不需設定路由器,不需公網ip,不需固定ip,不需動態域名,成功率90%以上,適合在公司,小區寬頻,出租屋,校園網,網咖,教育網,等網路結構複雜,限制嚴格的環境中使用。簡介 區域網路通...
宮,商,角,變角,徵,羽,閏,分別對應1,2,3,4,5,6,降7,閏是宮音下方的大二度。歌詞套用 宮、商、角、徵、羽雖為我國古代音階中的五音,而且也在音樂學上經常使用,但在現在歌詞里則常用到這五字,其中比較著名的...
則Q,., ( R)構成一個以[R,1]為單位元的環,稱為R的極大商環.對任意rER,若:二:R-R為右乘映射,則r-[R, r,]為R到Qn, ( R)的同構嵌人,即Q,n ( R含R為子環.上述方法是內海於1956年構造的.若R是奧爾環,則由R所...
如果兩個三角形有兩組對應邊和這兩組邊所夾的角相等,則兩三角形全等。(SAS)三角形面積是任一同底同高之平行四邊形面積的一半。任意一個正方形的面積等於其二邊長的乘積。任意一個矩形的面積等於其二邊長的乘積(據輔助定理3)。證...
點的張量。這樣才能定義張量場在映射意義下的微商。推導 一般形式 由引入中的平移以及向量的概念,可以初步定義李微商是 這樣一來,需要先把 的意義先確定下來。顯然, 式已經表明, 階張量的李微商仍是 階的張量。先看標量場 ...
“商音不應”即為“律呂音異”,治法“先補肝俞”,再“刺肺之所行”。《靈樞·五音五味》亦有記載“右徵與少徵,調右手太陽上;左商與左徵,調左手陽明上…判角與少角,調右足少陽下”,五音分出的二十五音可以調節相對應的...
有一個“自然”滿射群同態 π : G → G / N,把每個 G 的元素 g 映射到 g 所屬於的 N 的陪集上,也就是: π(g) = gN。映射 π 有時叫做“ G 到 G / N 上的規範投影”。它的核是 N。在包含 N 的 G 的子群...
(2)設X是BCI商代數,≠ 包含於X,稱作X的理想。若 蘊含 成立,這裡 。設 ≠ ,表示H的冪集,,H上的二元超代數運算“”定義為 ,即對於任意的 ,都有下面各式成立:(3)設 f 為BCI商代數 到BCI商代數 的同態映射,則...
