哥德爾運算屬於數學術語。
基本介紹
- 中文名：哥德爾運算
- 外文名：Godel operations
- 所屬學科：數學
哥德爾運算（Godel operations）用於構造集的基本運算.設.
哥德爾運算
｛（w,u）Ex｝，則稱由上列十種運算及它們的有限次複合構成的函式為哥德爾運算.哥德爾運算是美籍奧地利數學家哥德爾(Godel , K.)於1940年重新修改可構造集全域I的定義時引人的。
哥德爾運算
相關詞條
- 哥德爾運算
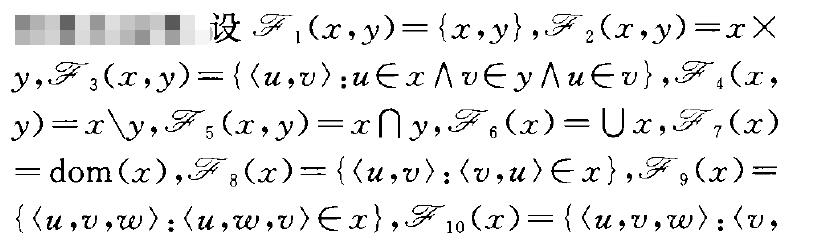
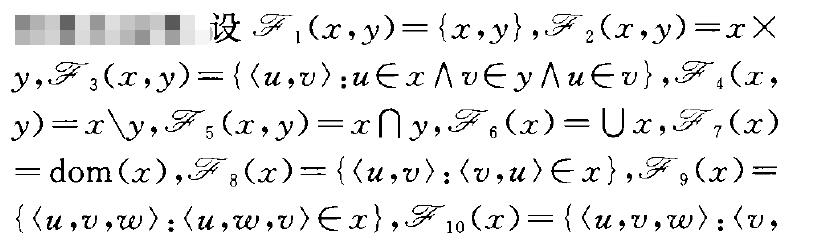
哥德爾運算屬於數學術語。哥德爾運算（Godel operations）用於構造集的基本運算.設.｛（w,u）Ex｝，則稱由上列十種運算及它們的有限次複合構成的函式為哥德爾運算.哥德爾運算是美籍奧地利數學家哥德爾(Gode...
- 哥德爾不完全性定理(2019年科學出版社出版的圖書)
《哥德爾不完全性定理》是2019年科學出版社出版的圖書，作者是（美）雷蒙德·M.斯穆瑞安（Raymond M.Smullyan）。內容簡介 《哥德爾不完全性定理》主要介紹哥德爾不完全性定理，在用簡單例子解說哥德爾的本質思想的基礎上，證明了基於加、乘及冪的塔斯基算術定理和基於加與乘的皮亞諾算術系統的不完全性定理，給出了...
- 數學女孩3:哥德爾不完備定理
《數學女孩3：哥德爾不完備定理》是2020年3月人民郵電出版社出版的圖書，作者是[日]結城浩。內容簡介 《數學女孩》系列以小說的形式展開，重點描述一群年輕人探尋數學中的美。內容由淺入深，數學講解部分十分精妙，被稱為“絕贊的數學科普書”。《數學女孩3：哥德爾不完備定理》有許多巧思。每一章針對不同議題進行...
- godel定理
這樣的一個形式化體系稱為一階算術，或者基本算術。其中只有求和以及相乘兩種運算。在這樣的算術體系中，素數是沒有意義的概念。這個體系中全部的記號、定義、規則都已經給出了，不能再加入新的對象。加入新的定義，比如定義素數，得到的將是另一個形式體系。當然新的形式體系可以看作基本算術體系的一個擴張。Godel不...
- 算術表示定理
這也是“算術分層”與“算術關係”一詞的來源。算術表示定理是美籍奧地利數學家哥德爾(Godel,K.)於 1931 年證明的。算術關係 算術關係是可以通過對遞歸關係添加有窮個量詞定義的關係。算術關係可以表示 形的關係，其中R為遞歸關係，為一階量詞∃或ᗄ。等價地，算術關係亦是可以從遞歸關係出發，經有限次否定與射影...
- 可構造集全域
可構造集全域(u niverse of constructible sets) 一種可構造集模型.美籍奧地利數學家哥德爾 (Godel , K.)用於證明連續統假設與選擇公理的相容性所構造的ZF系統模型，也是ZF系統的最重要的內模型.令Def (x)表示通過對x及x的元素進行有限次哥德爾運算所能得到的x的全部子集，即 其中c1 (M)表示M的哥德爾閉包，稱...
- 序數可定義集
則稱A為序數可定義集.但這種定義不能在集合論語言中形式化,形式的定義方式可利用哥德爾運算的概念定義序數可定義集.設c1 ( M)表示集合M的哥德爾閉包,R(a)為V的良基聚積分層(參見“良基聚積分層”),On表示所有序數構成的真類,則稱 公式 為序數可定義全域,oD的元素稱為序數可定義集. AEOD,若且唯若存在一個分...
- 算術關係
指算術關係可用一階算術公式表示的定理。它指出：一關係 為算術關係(即R在算術分層中)，若且唯若 在一階算術中可定義.即存在一階算術中的公式 ，使得對任何自然數 ，為真，若且唯若 在一階算術中為真，這也是“算術分層”與“算術關係”一詞的來源，算術表示定理是美籍奧地利數學家哥德爾()於1931年證明的。
- 丘奇定理
在理論計算機科學中，有了可計算性概念嚴格的數學刻劃，才使證明一系列重要的數學問題的算法不可解性成為可能。一個眾所周知的事實是，直到1935年著名的“算法可計算函式都是遞歸函式”這一丘奇論題提出，算法可計算性這個直觀概念才有了精確的數學刻劃。概念釋義 而同樣需要指出的是，哥德爾(K.Gödel)在此...
- 計數器機
三個計數器機的計算能力是等價的 -- 一個模型的指令可以從其他模型的指令得出。都等價於圖靈機的計算能力(但只有用哥德爾數來編碼在計算器中的數據，否則它們的能力等價於原始遞歸函式)。由於它們的一元處理方式，計數器典型的要比圖靈機慢一個因子，它是在相比較的圖靈機使用的空間的指數。計數器機模型還有一些...
- 可構造性公理
例如，不能一一定義出P(ω)中的所有元素，否則P(ω)的基數就可以輕鬆地確定下來，從而也就可以解決連續統假設問題，為了限制冪集運算，哥德爾利用“可定義冪集”取代冪集，所謂一個集合x的可定義冪集Def(x)，指包含能用集合論語言定義出的所有x的子集(參見“可構造集全域”)，因此，一旦x已知，則Def(x)中的...
- 邏輯演算
哥德爾完備性定理（見一階邏輯）及哥德爾不完備性定理等都是關於形式系統性質的定理。又如希爾伯特第 1問題即連續統假設問題的研究就是在集合論公理系統形式化的基礎上才廓清了問題，並取得了進展。因此，數理邏輯中對形式系統的研究也給數學研究開闢了新的途徑。那種認為建立邏輯演算的形式系統是為了進行形式思維，或者...
- 謂詞演算
謂詞演算最主要是在一階謂詞上的運算，下面列出了相關的一些重要的關於是否可判定的元邏輯定理。不像命題演算，一階邏輯是不可判定性的。對於任意的公式 P，可以證實沒有判定過程，判定 P 是否有效，（參見停機問題）。有效性的判定問題是半可判定的。按哥德爾完備性定理所展示的，對於任何有效的公式 P,P 是可...
- algorithm(計算機術語)
這些嘗試包括庫爾特·哥德爾、雅克·埃爾布朗和史蒂芬·科爾·克萊尼分別於1930年、1934年和1935年提出的遞歸函式，阿隆佐·邱奇於1936年提出的λ演算，1936年埃米爾·萊昂·珀斯特的Formulation 1和艾倫·圖靈1937年提出的圖靈機。即使在當前，依然常有直覺想法難以定義為形式化算法的情況。特徵 以下是高德納在他的著作...
- 高階邏輯
高階邏輯更加富有表達力，但是它們的性質，特別是有關模型論的，使它們對很多套用不能表現良好。作為哥德爾的結論，經典高階邏輯不容許（遞歸的公理化的）可靠的和完備的證明演算；這個缺陷可以通過使用Henkin模型來修補。高階邏輯的一個實例是構造演算。套用 高階邏輯在數學中，高階邏輯在很多方面有別於一階邏輯。
- 數理邏輯史
1931年K.哥德爾發表著名論文《〈數學原理〉及有關係統中的形式不可判定命題》，嚴格地證明了：如果一個包括初等數論的形式系統是一致的，那么其一致性不能用有窮方法甚至不能用一階謂詞演算和初等數論的方法證明。此定理給希爾伯特方案以沉重打擊。希爾伯特等人隨即決定將有窮方法稍加擴充，增加超窮歸納作為元數學的...
- 部分遞歸函式
經代入或一般遞歸作用而得。這個序列也稱為φ的遞歸描述。從而，任何部分遞歸函式都有其遞歸描述。利用哥德爾編碼技巧，對任何遞歸描述都可進行能行編碼。相應地，全體部分遞歸函式也可能行編碼，由此可以給出全體部分遞歸函式的一種能行枚舉，通常以 表示全體n元部分遞歸函式的一種能行枚舉，e稱為 的下標，在元數...
- 丘奇論題
Lambda可定義函式由阿隆佐·邱奇和史蒂芬·克萊尼（Church 1932, 1936a, 1941, Kleene 1935）提出，而遞歸函式由庫爾特·哥德爾（Kurt Gödel）和雅克·埃爾布朗（Jacques Herbrand，Gödel 1934, Herbrand 1932）提出。這兩個機制描述的是同一集合的函式，正如邱奇和克林（Church 1936a, Kleene 1936）所展示的正...
- 邱奇數
在其他符號系統中通常被認定為基本的項（比如整數、布爾值、有序對、列表和tagged unions）都被映射到使用 邱奇編碼的高階函式；根據邱奇-圖靈論題我們知道任何可計算的運算符（和它的運算數）都可以用邱奇編碼表示。很多學數學的學生熟悉可計算函式集合的哥德爾編號；邱奇編碼是定義在lambda抽象而不是自然數上的...
- 可構造性
)的基數就可以輕鬆地確定下來，從而也就可以解決連續統假設問題.為了限制冪集運算，哥德爾利用“可定義冪集”取代冪集.所謂一個集合x的可定義冪集Def (x)，指包含能用集合論語言定義出的所有x的子集(參見“可構造集全域”)，因此，一旦x已知，則Def(x)中的每個元素也可描述.令L(0)=O,L(a-1)=Def(L(a)...
- 單泛代數
由於數理邏輯的發展，為泛代數的研究提供了一個新的工具，特別是哥德爾完全性定理、塔爾斯基可滿足性概念、緊緻性定理等，使人們意識到邏輯在代數中套用的可能性。馬爾茨夫(Malcev)於1941年發表了這方面的第一篇論文，由於戰爭，他的論文沒有引起人們的注意。後來，塔爾斯基(Tarski，A.)、亨金(Henkin，L.)和魯賓孫...
- 公理集合論
由哥德爾不完備性定理可知：如果ZF是協調的，則在ZF中不能證明自身的協調性。所以，在公理集合論中只考慮相對協調性問題。如：解決這類問題的常用方法就是構造模型。在公理集合論中構造模型的方法不外三點：內模型法，外模型法（即力迫方法），對稱模型法。內模型法是從已知的一個模型M 出發，來定義M 的一個子...
- 反射原理
20世紀30年代哥德爾、馬爾采夫等人在緊緻性定理方面的工作也是重要的奠基性工作。但是直到20世紀50年代，模型論才正式成為一門新的學科，主要標誌是1949年亨肯發表的完全性定理的新證明，1950年國際數學家大會上塔爾斯基與A.魯賓遜的報告以及1951年A.魯賓遜《代數的元數學》的發表。一個形式語言ℒ的解釋u稱為此語言的...
- 能行性和一般遞歸
在這演算內可以表示自然數，並且利用運算子λ而作出了λ可定義函式,其中包括原始遞歸函式。1934年,K.哥德爾根據J.赫爾布蘭德的一個建議，提出了一般遞歸函式。其定義是：如果能夠作出一組方程式，使得只利用變元代以常數以及相等的數可以彼此替換兩個過程，便能夠導出函式f的一切值，而函式f便叫做一般遞歸函式。不久，...
- 判定問題
20世紀30年代，哥德爾證明了謂詞演算的完全性，和算術系統的不完全性等重要結論，使數理邏輯成為一門獨立的學科。它對於公理化方法、數學基礎及某些數學分支的研究，都具有重要的作用，它還是控制論與計算機科學的基礎理論之一。在計算機技術、人工智慧、語言學、自動化系統及開關線路中得到廣泛的套用，同時它本身也隨之...
- 算法(解題方案的準確而完整的描述)
這些嘗試包括庫爾特·哥德爾、Jacques Herbrand和史蒂芬·科爾·克萊尼分別於1930年、1934年和1935年提出的遞歸函式，阿隆佐·邱奇於1936年提出的λ演算，1936年Emil Leon Post的Formulation 1和艾倫·圖靈1937年提出的圖靈機。即使在當前，依然常有直覺想法難以定義為形式化算法的情況。特徵 一個算法應該具有以下五個重要...
- 多值邏輯
哥德爾在1932年證明了直覺邏輯不是有限多值的邏輯，並定義了在經典邏輯和直覺邏輯之間的哥德爾邏輯系統，這種邏輯叫做中間邏輯。建立及套用 多值邏輯建立於20世紀20年代初，由盧卡西維茨和美國邏輯學家E.L.波斯特創建。盧卡西維茨在其1920年發表的《論三值邏輯》一文中，建立了一個三值邏輯系統。波斯特在其1921年發表...
- 數學危機
為了排除集合論悖論，羅素提出了類型論，策梅羅提出了第一個集合論公理系統，後經弗倫克爾加以修改和補充，得到常用的策梅羅——弗倫克爾集合論公理體系，以後又經伯奈斯和哥德爾進一步改進和簡化，得到伯奈斯——哥德爾集合論公理體系。希爾伯特還建立了元數學。作為對集合論悖論研究的直接成果是哥德爾不完全性定理。美國...
- 完全格
由於數理邏輯的發展，為泛代數的研究提供了一個新的工具，特別是哥德爾完全性定理、塔爾斯基可滿足性概念、緊緻性定理等，使人們意識到邏輯在代數中套用的可能性。馬爾茨夫(Malcev)於1941年發表了這方面的第一篇論文，由於戰爭，他的論文沒有引起人們的注意.後來，塔爾斯基(Tarski，A.)、亨金(Henkin，L.)和魯賓孫...
