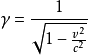在古典力學中，向心力是當物體沿著圓周或者曲線軌道運動時，指向圓心（曲率中心）的合外力作用力。“向心力”一詞是從這種合外力作用所產生的效果而命名的。這種效果可以由彈力、重力、摩擦力等任何一力而產生，也可以由幾個力的合力或其分力提供。
因為圓周運動屬於曲線運動，在做圓周運動中的物體也同時會受到與其速度方向不同的合外力作用。對於在做圓周運動的物體，向心力是一種拉力，其方向隨著物體在圓周軌道上的運動而不停改變。此拉力沿著圓周半徑指向圓周的中心，所以得名“向心力”。向心力指向圓周中心，且被向心力所控制的物體是沿著切線的方向運動，所以向心力必與受控物體的運動方向垂直，僅產生速度法線方向上的加速度。因此向心力只改變所控物體的運動方向，而不改變運動的速率，即使在非勻速圓周運動中也是如此。非勻速圓周運動中，改變運動速率的切向加速度並非由向心力產生。
向心力的大小與物體的質量（m）、物體運動圓周半徑的長度（r）和角速度（ω）有著密切關係。
基本介紹
- 中文名：向心力
- 外文名：centripetal force
- 表達式：F=Mω2r
- 套用學科：物理
- 適用領域範圍：力學、運動學
- 適用領域範圍：機械
公式,相關知識,分類,
公式
質量為m的物體以速度v沿曲率半徑為r的曲線運動時所需的向心力F為：
其中：v為線速度 單位m/s，ω為角速度 單位rad/s，m為物體質量 單位kg，r為物體的運動半徑 單位m，T為圓周運動周期 單位s，f為圓周運動頻率 單位Hz，n為圓周運動轉速（即頻率）單位r/s。
在粒子加速器中，粒子的速度接近於真空中的光速，考慮到相對論效應，向心力的表達式為：
相關知識
（1）向心力是從力的作用效果來命名的，因為它產生指向圓心的加速度，所以稱它為向心力。它不是具有確定性質的某種類型的力。相反，任何性質的力都可以作為向心力。實際上它可是某種性質的一個力，或某個力的分力，還可以是幾個不同性質的力沿著半徑指向圓心的合外力。
（2）向心力為何不把物體拉向圓心
做圓周運動的物體，速度方向時刻要改變，為了改變物體速度的方向，需要一定大小的力，構想物體沒有受力，那么在慣性作用下不是會沿著切線方向飛出去嗎？而物體做圓周運動時，向心力的大小恰好就等於所需要的力，因而它沒有“餘力”把物體拉向圓心。實際上，給予的拉力大於所需的向心力，就確實會把物體拉向圓心，而如果所給予的力小於所需的向心力，就會在水平切線方向有一個分速度，從而令運動的物體做偏離圓周軌道的曲線運動。
（3）勻速圓周運動（曲線運動）是變速運動
勻速圓周運動的速度方向時刻改變，必定存在加速度．從運動學角度可以證明，做勻速圓周運動的物體的加速度大小為a=v2/r=ω2r，方向總是指向圓心，因此勻速圓周運動的加速度，叫向心加速度。向心加速度總與速度垂直.只改變線速度的方向，不改變線速度的大小.方向與向心力相同，指向圓心。
（3）有沒有離心力？
假設若離心力存在，則與向心力相平衡，物體受力平衡，速度方向不會改變，是平衡態，不可能做圓周運動，所以證明離心力並不存在，即離心力是以力的作用效果來命名的。
分類
勻速圓周運動和非勻速圓周運動
圓周運動按照速度大小是否變化可分為勻速圓周運動和非勻速圓周運動兩類。
做勻速圓周運動的物體，速度大小不變，只是方向改變，因此加速度總是指向圓心，其大小不變；合外力亦總是指向圓心，大小不變。
做非勻速圓周運動的物體，速度方向和大小均變，它除了有指向圓心的加速度外，還有沿切線方向的加速度，所以合加速度不指向圓心，所受合外力也不指向圓心。物體的向心加速度大小a=v2/r隨v值變化，向心力a隨F=ma值變化．例如，小球沿豎直平面內的光滑圓軌道運動，如圖所示，球從上向下通過A點時的受兩個力作用，其中重力G方向與Va相同，使小球速度大小發生變化，軌道彈力N與Va垂直，指向圓心，使小球速度方向發生變化，即提供小球做圓周運動的向心力，合力F與Va成一角度，並不指向圓心。
變速圓周運動
中向心力大小不恆定
在勻速圓周運動中，合外力不改變線速度大小，只改變線速度方向，向心力即為物體所受的合外力；在變速圓周運動中，合外力一方面要改變線速度的大小，另一方面要改變線速度的方向，所以向心力不一定等於物體所受的合外力，並且由於變速圓周運動線速度大小不恆定，所以變速圓周運動中向心力大小不恆定。
