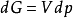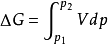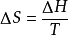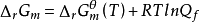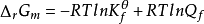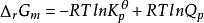吉布斯自由能變

按照國際純粹與套用化學聯合會( IUPAC)的定義，吉布斯自由能或吉布斯函式是焓(H)減去熱力學溫度(T)和熵(S)的乘積，即G=H-TS，常稱為自由能或自由焓。其 SI 單位為焦耳(J)。與其他熱力學函式一樣，G也具有狀態函式的屬性。由於H絕對值未知故G的絕對值也是不可知的，但其變化量即ΔG只決定於系統的始態和終態，而與變化的具體途徑無關。吉布斯自由能具有廣泛的功能特性，如在等溫、等壓條件下可作為反應自發進行方向的判據，還具有狹義化學勢、最大非膨脹功和狹義表面自由能等功能。這些功能特性往往都是以其改變數ΔG來體現的。

基本介紹

• 中文名：吉布斯自由能變
• 外文名：The gibbs free energy change
• 性質：化學名詞
• 決定於：系統的始態和終態
• 定義：吉布斯自由能的變化量
• 特點：與變化的具體途徑無關
• 作用：判定反應方向

簡介

吉布斯自由能G是物理化學中非常重要、套用非常廣泛的一個熱力學狀態函式。它的絕對值的大小我們沒有辦法得知，而其改變數△G卻可以通過一定方法進行計算，且△G的計算在一定程度上顯得更為重要。因為吉布斯自由能G雖然是在熱力學第一定律和第二定律的基礎上，在定溫定壓條件下經過一定的熱力學推導而定義的一個熱力學狀態函式，但並不是只有在定溫定壓條件下的系統才有吉布斯自由能，也不是只有在定溫定壓下系統狀態發生變化時才有吉布斯自由能變△G，而是在任意條件下，當系統處於一定狀態時就有確定的吉布斯自由能G，當系統的狀態發生改變時就有吉布斯自由能變△G的存在，無論是簡單的狀態變化過程，還是複雜的化學變化過程和相變化過程都是如此。我們知道，△G可用於判斷定溫定壓下各種熱力學過程自發進行的方向和限度，而在實際過程中常遇到的各種熱力學過程往往是在定溫定壓條件下進行的。因此，雖然熱力學判據較多，如熵判據，亥姆霍茲自由能判據等。而吉布斯自由能變△G作為判據更為有利和方便。

單純狀態變化過程中的計算

理想氣體定溫過程

對於理想氣體狀態變化，可根據熱力學的基本公式dG=-SdT+Vdp ，定溫過程dT=0，則有 ，積分可得 ，即根據此式可直接計算△G，再根據△G的正負來判斷過程的自發性。

理想氣體混合過程

若熱力學系統是由兩種或兩種以上理想氣體混和而成，且每種氣體單獨存在時的溫度和壓力相等且等於混和氣體的溫度和壓力，則該混和過程中吉布斯自由能變可根據 進行計算，式中n_i為系統中i組分的物質的量，x_i為系統中i組分在混和氣體中的物質的量分數，T為系統的溫度，R為氣體常數。

非理想氣體系統定溫過程

對於非理想氣體系統，△G的計算，一方面可以用，只要找出系統中V與P之間的函式關係式，將V用含P的關係式代替代入公式，積分求解即可得△G。另一方面，可根據△G=△H一T△S。△H的 利用上式便可方便求出過程的△G，進而根據△G的正負判斷過程的自發性。

相變化過程中的計算

相變化過程可分為兩種情況。一種是系統在發生相變化的過程中始態和終態的兩個相始終是平衡的，即系統發生的是可逆相變化，另一種情況是系統在發生相變化的過程中始態和終態的兩個相是不平衡的，即為不可逆相變化過程。系統發生相變化的方式不同，其吉布斯自由能變△G的計算方法也有所區別。

可逆相變過程中

對於可逆相變化過程，由於它是在溫度和壓力一定的條件下進行的，由△G=△H一T△S，△H是可逆相變熱，△S是可逆相變時的熵變。 ，因此，可逆相變過程中吉布斯自由能變 。故當系統發生可逆相變化時，無需計算，△G=0，反過來，如果某一相變化過程中△G=0，則該系統所發,生的相變化一定為可逆相變。

不可逆相變過程中

對於不可逆相變過程，直接計算該過程的△G是不可能的。但這並不意味著該過程的△G無法計算，因為我們總可以將不可逆相變過程設計為始態和終態與此不可逆相變過程相同的可逆過程，然後直接利用公式進行計算。

反應方向判據

若系統在等溫、等壓且不做非膨脹功的條件下，其變化值可以表示為-ΔG≥ 0或ΔG≤ 0，即自發變化總是朝著Gibbs自由能減少的方向進行，直至平衡為止。系統不可能發生ΔG> 0的變化。Gibbs自由能的變化值可作為等溫、等壓且不做非膨脹功條件下自發變化方向的判據。由於大多數反應都是在等溫、等壓條件下進行，與其他判據相比，Gibbs自由能判據更為常用。

對於任意化學反應，其變化方向可通過化學反應的等溫方程式（van′t Hoff等溫式）進行判斷，即

或 （Q_f表示反應系統的逸度商，K^θ_f為系統的熱力學平衡常數）。通過比較Q_f和K^θf數值的相對大小，即可獲得ΔrGm< 0、ΔrGm= 0或ΔrGm> 0的結果，並可以此判斷化學變化的方向。

在理想氣體混合物系統中，由於Q_f= Q_p，K^θ_f= K^θp，化學反應等溫式可表示為：

若K^θp> Q_p，則Δ_rG_m< 0，表示正向反應自發進行；

若K^θp= Q_p，則Δ_rG_m= 0，表示系統已處於平衡狀態；

若K^θp< Q_p，則Δ_rG_m> 0，表示對於給定反應式，反應不能向右自發進行。

狹義表面自由能

在表面物理化學的研究中，在指定各相應變數不變的情況下，每增加單位表面積時，系統熱力學能或Gibbs自由能等熱力學函式的增加值稱為廣義表面自由能。而狹義表面自由能是指，當以可逆方式形成新表面時，環境對系統所作的表面功變成了單位表面層分子的Gibbs自由能。

基於Gibbs自由能所具有的狹義表面自由能的性質，可以對很多實際系統進行分析。例如，在膠體分散系統中，其聚結過程是熱力學的自發過程，即ΔG < 0，當表面張力γ為恆值時，ΔA< 0，即要縮小表面，只有通過聚結或聚並作用。在實際系統的研究中，為獲得穩定的膠體體系，常需要加入分散穩定劑（如高分子、表面活性劑等），在膠體表面形成表面結構層，以達到縮小表面的作用；另外，加大空間位阻，可以避免膠體粒子之間的聚結或聚並作用的發生，達到穩定膠體的目的。

選用高分子物質作為膠體系統的分散穩定劑時，當濃度和相對分子質量合適時，吸附在膠體顆粒表面的高分子物質可以降低膠體的表面能，有效避免顆粒聚集過程的發生，使膠體顆粒穩定。當高分子物質濃度較低時，不能將每個膠體顆粒包住，反而起到架橋作用，使顆粒間產生吸引作用，最終發生絮凝。因此，在很多實際體系中，如污水處理，高分子絮凝劑在加入量少時容易發生絮凝，而加入量多時可以起到保護膠體的作用。另外，利用分散製備法獲得固體分散體系時，常加入表面活性劑來穩定膠體顆粒。表面活性劑的加入，不僅能降低表面張力，而且在膠體顆粒表面形成溶劑化膜或雙層膜，達到降低膠體顆粒表面能的作用，使得膠體顆粒更穩定。

吉布斯自由能的生物學意義

從吉布斯自由能的物理意義可以了解其生物學意義，在可逆的等溫等壓過程中 ，這表明，在等溫等壓過程中，系統吉布斯自由能的減少等於除去體積膨脹功以外，系統對外界所作的功。根據功能原理容易理解，系統的吉布斯自由能是指系統總能量中能作除膨脹功以外的其他有用功的那部分能量。由於生命體系中發生的絕大多數過程(化學反應過程、生理過程等等)都是在等溫等壓下進行的，因此，對生命體系而言，吉布斯自由能就是生命體系在等溫等壓條件下維持正常運轉所需要的最小能量。那么，生命體系中的吉布斯自由能從何而來?它又是如何運轉的呢?

眾所周知，植物通過光合作用俘獲光能，利用光能合成碳水化合物，碳水化合物在體內經過分解代謝逐漸放出能量，再用此能量驅動生命過程的進行。因此，碳水化合物分解放出的能量就是吉布斯自由能，而太陽則是生命體系吉布斯自由能的唯一來源。據計算，1mol葡萄糖完全氧化時放出的吉布斯自由能約為2879kJ，利用這個能量，動植物可以產生總量為38mol的高能化合物三磷酸腺苷(ATP)，這些ATP作為能量的貨幣再被用於維持細胞生存。

另一方面,，就吉布斯自由能的變化而言，如前所述，它可以作為判斷等溫等壓過程能否自發進行的判據。由於生命體系內發生的過程大都是等溫等壓過程，因此，吉布斯自由能的這一功能對於生命過程也具有實際意義。在生命體系中，為了保證某一過程能夠自發進行，常常進化出一些偶聯反應，通過反應之間的偶聯滿足ΔG< 0的條件，從而使一些單獨無法自發進行的過程變得可以自發進行。例如，在動植物體

系的呼吸代謝中，大量存在的葡萄糖和無機磷生成6-磷酸葡萄糖的反應，其ΔG= 17.1 kJ/mol。由於ΔG>

0，這一反應過程是不能自發進行的，但是，如果偶聯一個三磷酸腺苷和水生成二磷酸腺苷與無機磷的反應,這一反應的ΔG= - 30.5 kJ/mol。兩個反應偶聯。總的吉布斯自由能變ΔG= 17.1+(- 30.5)= - 13.4(kJ/mol)< 0，從而使得6-磷酸葡萄糖的生成反應可以自發進行。由此也就容易理解生命體系中存在大量偶聯反應的原因了。看來，偶聯反應是生命過程滿足ΔG< 0的必要條件。

總之，吉布斯自由能對於生命體系是至關重要的。就吉布斯自由能本身而言，它作為生命體系賴以生存的能量，直接維持和驅動著生命體系的運轉；就吉布斯自由能的變化而言，它可以作為生命過程能否自發進行的判據。