可換BCI代數(commutative BCI-algebra)可換BCK代數的一種推廣.
設X是BCI代數，若d x,yEX，有
則稱X為可換BCI代數.可換BCK代數與p半單BCI代數都是可換BCI代數，反之不真.設X是BCI代數，X的極小元a(即若二*a=。則二=a)所確定的子集V (a)= {xE X } aGx}稱為X的分支.若BCI代數的每個分支V<a)都有最大元ma，則稱X為局部有界的.局部有界可換BCI代數X的每個分支V (a)都是一個分配格.
可換BCI代數
相關詞條
- 可換BCI代數
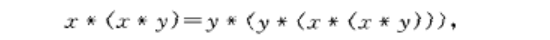
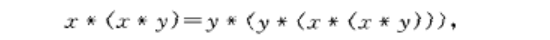
可換BCI代數(commutative BCI-algebra)可換BCK代數的一種推廣...... 可換BCI代數(commutative BCI-algebra)可換BCK代數的一種推廣.設X是BCI代數,若d x,yEX,有...
- 擬可換BCI代數
擬可換BCI代數(quasi-commutative BCI-aI-gebra)交換和正關聯BCI代數的一種共同推廣.設(X;*,0>為BCI代數,記若d x,yEX,存在著非負整數m,n,s,t,使Q>a,...
- 可分解BCI代數
(decomposable BCI-algebra)一類BCI代數.它是可直和分解的.設X是BCI代數,若X的每一個子代數都是X的理想,則稱X為可分解BCI代數.p半單BCI代數是可分解BCI代數,...
- 具有條件BCI代數
具有條件BCI代數是一類重要的BCI代數,是於1977年引進了具有條件(:)的BCK代數,1980年又推廣到BCI代數上去,並奠定了它的基礎理論.具有條件(s)的關聯BCK代數與冪等...
- BCI-代數與半群
《BCI-代數與半群》是2011年科學出版社出版圖書,作者是楊聞起。...... 《BCI-代數與半群》是一本研究BCI-代數與群、半群、環和半環的關係的著作,共有5章,...
- 純BCI代數
純BCI代數(pure BCI-algebra ) BCK代數的“單純”擴張(僅添加p半單部分).設X是BCI代數,P(X>={二EX{x,0};Q(二)一{xEX}0*(0*二)=x},若X=P(X) ...
- 關聯BCI代數
關聯BCI代數(implieative BCI-algebra)關聯BCK代數的一種推廣.設X是BCI代數,若d二,yEX,有 (x*(x*y))*(y*x)=y*(y*x), 則稱X為關聯BCI代數.關聯BCK...
- 雙B代數
雙B代數(BCK-algebra and BCI-algebra orTwo-B-algebras ) BCK代數與BCI代數的簡稱,它是序代數中一門新興的有廣泛套用的分支學科。...
- 完全BCI代數
(complete BCI-algebra)一類BCI代數.它是非空子集具有上、下確界的BCI代數.設X是BCI代數,若X的每一個非空子集A在X中存在最小上界與最大下界,則稱X為完全...
- 自由BCI代數
自由BCI代數(free BCI-algebra)一類與自由代數相仿的有生成元集的BCI代數.設X是一非空集合,BCI (BCK)代數T稱為由X生成的自由BCI (BCK)代數,若存在映射f : ...
- 結合BCI代數
結合BCI代數(associative BCI-algebra)一類重要的BCI代數.它是關於運算二滿足結合律的BCI代數.設(X;*,0)是BCI代數,d二,y,zEX,若(二‘必*z=二二(y二z)...
- 有界BCI代數
有界BCI代數(bounded BCI-algebra)是一類重要的BCI代數。...... 有界BCI代數(bounded BCI-algebra)是一類重要的BCI代數。它是有上界的BCI代數.若BCI代數<X; * ...
- 廣義擬左交錯BCI代數
廣義擬左交錯BCI代數(generalized quasi leftalternating BCI-algebra)擬交錯BCI代數的一種推廣.設X是BCI代數,對任意x, yCX,x}y,若滿足條件x-y,則稱X是廣義擬...
- 正則BCI代數
正則BCI代數(regular BCI algebra)一類特殊的BCI代數.設(X;},。)是BCI代數,A,B是X的任意兩理想,若對任意的二,yE (AUB)均有ArnBy}s},則稱x為正則BCI代數...
- 半單BCI代數
半單BCI代數(semi-simple of BCI-algebras )BCI代數的重要子類.指每個理想均為一次直和項的BCI代數.若BCI代數X的任一理想是X的次直和項,則稱X為半單的.非...
- 擬左(右)交錯BCI代數
擬左(右)交錯BCI代數(quasi left (right) al-ternating BCI-algebra)一類BCI代數.它滿足左右交錯律.若對BCI代數<X; y, 0>中任意不同的x,y均有x*(x*必...
- 正關聯BCI代數
正關聯BCI代數(positive implicative BCI-aI-gebra)正關聯BCK代數的一種推廣。...... 正關聯BCI代數(positive implicative BCI-aI-gebra)正關聯BCK代數的一種推廣。...
- 局部有限代數
局部有限代數(locally finite algebra)與局部有限群相平行的概念。若域F上代數A...局部有限的BCI-代數[J]. 昭通師專學報,1994,(03):20-25. ...
- BCI-代數
《BCI-代數》是2007年科學出版社出版的圖書。...... 《BCI-代數》內容簡介:This book is mainly designed for the graduate students who are in-terested in t...
- BCI代數理想
BCI代數理想(ideal of BCI-algebra)亦稱BCI代數的幻.BCI代數中的特殊子集.它是含零元且不同於子代數的能誘導出商結構的子集.BCI代數(X;、,0>的一個非空子...
- BCI代數元素周期
BCI代數元素周期(period of element inBCI-algebra)相似於群的元素的周期.設X是BCI代數,xEX,稱使。* x..。的最小自然數n為x的周期.若這樣的n不存在,則稱...
- P半單BCI代數
P半單BCI代數(p scmisimplc BCI algebra)一類重要的BCI代數。...... P半單BCI代數(p scmisimplc BCI algebra)一類重要的BCI代數。若X是BCI代數,則分別稱...
- J半單BCI代數
J半單BCI代數(J-semisimple BCI-algebra)類似於環論中J半單環.設X是BCI代數,稱為X的雅各布森根.若J(X)一{0},則稱X為J半單BCI代數.有界正關聯的對合(...
- 正關聯理想
正關聯理想(positive implicative ideal)亦稱正關聯幻.刻畫正關聯BCI代數的一種理想.設I是BCI代數X的子集.若滿足:0<I,則稱I是X的可換理想.BCK代數X稱為正...
- 楊聞起
使一般BCI-代數關於這個加法作成可換序半群,這不但統一前人的結論,而且建立起了一般BCI-代數與可換序半群的緊密聯繫;另一方面,在IS-代數中通過引入伴侶半環和...
