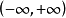反雙曲函式

反雙曲函式是雙曲函式的反函式。記為（arsinh、arcosh、artanh等等）。與反三角函式不同之處是它的前綴是ar意即area(面積)，而不是arc(弧)。因為雙曲角是以雙曲線、通過原點直線以及其對x軸的映射三者之間所夾面積定義的，而圓角是以弧長與半徑的比值定義。

基本介紹

• 中文名：反雙曲函式
• 外文名：inverse hyperbolic function
• 套用學科：數學
• 對比：雙曲函式
• 種類：6種
• 求導：兩大類

定義

我們知道，三角函式分為sin（正弦）、cos（餘弦）、tan（正切）、cot（餘切）、sec（正割）、csc（餘割）六種。而雙曲函式也如此。故而，反雙曲函式也有六種。有反雙曲正弦、反雙曲餘弦、反雙曲正切、反雙曲餘切、反雙曲正割、反雙曲餘割六種。這裡，就介紹比較常見的前三種：反雙曲正弦、反雙曲餘弦、反雙曲正切。

反雙曲函式是雙曲函式的反函式。記為（arsinh、arcosh、artanh等等）。與反三角函式不同之處是它的前綴是ar意即area(面積)，而不是arc(弧)。

反雙曲正弦

反雙曲正弦函式記作y=arsinhx。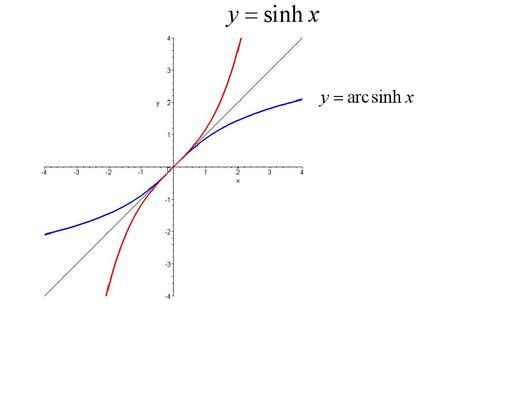

反雙曲正弦函式圖像

雙曲函式y=sinhx的定義是y=sinhx= .那么，取它的反函式，最終得到反雙曲正弦函式的定義是y=arsinhx= 。

反雙曲正弦函式的定義域為 。它是奇函式。在區間 內單調增加。反雙曲正弦函式的圖像如圖所示。

反雙曲正弦函式的導數是 。不定積分是 （不包含不定積分特有的常數C）。

反雙曲正弦函式的冪級數展開式是：

。

反雙曲餘弦

反雙曲餘弦函式記作y=arcoshx。

反雙曲餘弦函式圖像

雙曲函式y=coshx的定義是y=coshx= .那么，取它的反函式，最終得到反雙曲餘弦函式的定義是y=arcoshx= 。

反雙曲餘弦函式的定義域為 。它是非奇非偶函式。在區間 內單調增加。反雙曲餘弦函式的圖像如圖所示。

反雙曲餘弦函式的導數是 。不定積分是 （不包含不定積分特有的常數C）。

反雙曲餘弦函式的冪級數展開式是：

= 。

反雙曲正切

反雙曲正切函式記作y=artanhx。

雙曲函式y=sinhx的定義是y=tanhx= .那么，取它的反函式，最終得到反雙曲正切函式的解析式是y=artanhx= 。

反雙曲正切函式的定義域為 。它是奇函式。在區間 內單調增加。反雙曲正切函式的圖像如圖所示。

反雙曲正切函式的導數是 。不定積分是 （不包含不定積分特有的常數C）。需要注意，在反雙曲正切的不定積分中，有條件 ，此不定積分才能成立。

反雙曲正切函式的冪級數展開式是：

= 。

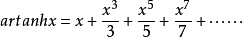
對比

在數學中，雙曲函式類似於常見的（也叫圓函式的）三角函式。基本雙曲函式是雙曲正弦“sinh”，雙曲餘弦“cosh”，從它們導出雙曲正切“tanh”等。

求導

雙曲函式求導

shx = (e^x - e^(-x)/2, (shx) ' =chx
chx = (e^x + e^(-x)/2, (chx) ' =shx
thx = shx / chx, (thx) ' = 1/(chx)^2

反雙曲函式求導

arsinh x = ln[ x+ (x^2+1)^(1/2) ] , (arsinh x) ' = 1/ (x^2+1)^(1/2)

arcosh x = ln[ x+ (x^2-1)^(1/2) ] , (arcosh x) ' = 1/ (x^2-1)^(1/2)

artanh x =(1/2) [ ln(1+x)/(1-x) ], (artanh x) ' = 1/(1-x^2)