博蘇克-烏拉姆定理

博蘇克-烏拉姆定理表明，任何一個從n維球面到歐幾里得n維空間的連續函式，都一定把某一對對蹠點映射到同一個點。

基本介紹

• 中文名：博蘇克-烏拉姆定理
• 外文名：Borsuk-Ulam Theorem
• 提出者：博蘇克-烏拉姆
• 套用學科：數學

簡介

博蘇克-烏拉姆定理是關於有限維空間中的連續奇映射的著名定理。

設X和Y是有限維賦范線性空間，且dim Y<dim X，S為X中的單位球面，f:S→Y為連續奇映射（f(-x)=-f(x),∀x∈S），則存在x∈S使f(x)=0。

博蘇克-烏拉姆定理表明，任何一個從n維球面到歐幾里得n維空間的連續函式，都一定把某一對對蹠點映射到同一個點。

發展

博蘇克-烏拉姆定理首先由烏拉姆猜想。1933年，Karol Borsuk證明了該定理。從博蘇克-烏拉姆定理可以推出布勞威爾不動點定理。

一個關於博蘇克-烏拉姆定理的更強的陳述，是每一個保持對蹠點的映射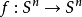，都具有奇次數。

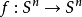
推廣

博蘇克-烏拉姆定理有許多推廣的形式。例如奇的全連續向量場（或凝聚向量場）的度數是奇數，奇的逼近固有映射的廣義度不含偶數。另一方面，奇映射即在群Z₂作用下等變的映射。

• Rⁿ的任何子集都不與Sⁿ同胚。
  
• 如果用n+1個開集來覆蓋球面Sⁿ，那么其中一定有一個開集含有一對對蹠點（與博蘇克-烏拉姆定理等價）。
  
• 火腿三明治定理（對於任何Rⁿ內的緊集A_{1，......，}A_n，我們總可以找到一個超平面，把每一個緊集都分成兩個具有相同測度的子集）。