基本介紹
- 中文名:半連續性
- 外文名:Semi-continuity
- 分類:數學分析
- 領域:數理科學
形式定義
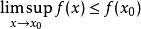
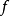
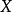
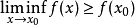
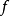
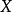
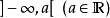
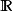
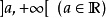
例子
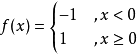
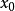
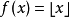
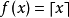
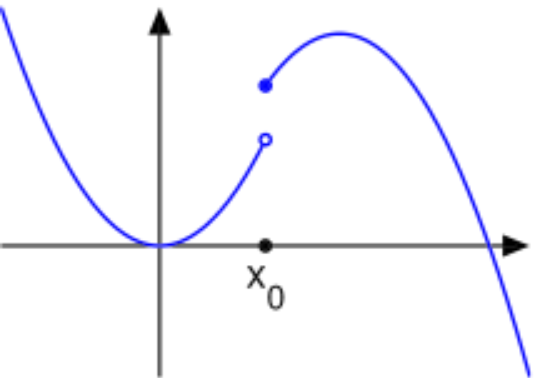 圖1 上半連續函式的例子
圖1 上半連續函式的例子 圖2 下半連續函式的例子
圖2 下半連續函式的例子性質
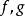
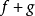
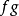
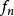
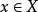
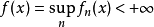
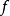
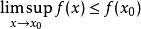
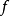
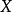
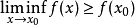
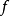
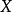
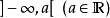
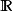
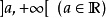
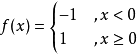
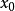
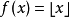
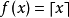
 圖1 上半連續函式的例子
圖1 上半連續函式的例子 圖2 下半連續函式的例子
圖2 下半連續函式的例子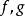
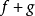
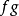
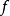
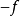
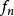
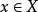
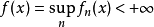
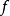
定義在拓撲空間E上的數值函式f稱為在E的點x0下(上)半連續,如果對滿足b<f(x0)(b>f(x0))的R上任一元素b,存在x0的鄰域V,使對V上的任一點x,b<f(x...
在數學分析中,半連續性是實值函式的一種性質,分成上半連續與下半連續,半連續性較連續性弱。...
半連續過程,是指物料在一段時間內連續加入,但連續操作間斷進行的一類化工加工過程。...
半連續乳液聚合工藝是首先將部分軟水、單體、乳化劑、調節劑和引發劑等助劑投入聚合釜,在聚合到一定程度後,再將其餘的介質水、單體和助劑在一定的時間間隔內連續地...
半連續發酵(semi-continuous fermentation),又稱半連續培養、反覆分批培養或換液培養,是指在分批培養的基礎上,周期性地放出部分含有產物的發酵液,然後再補加相同...
在一般拓撲學中,半連續映射是一類廣義連續映射。在泛函分析中,半連續映射即有限1-弱連續映射,是限制在定義域中過每點的一維線性流形上是連續的映射。...
半連續函式隔離定理陳述了可用連續函式將在各點有相同大小關係的上半連續函式與下半連續函式分隔開來的命題。...
▪ 凹函式與凸函式 ▪ 上半連續 ▪ 下半連續 3 相關性質 ▪ 線性組合 ▪ 定理1 ▪ 定理2 ▪ 定理3 ▪ 定理4 ▪ 定理5 連續...
鋼水經結晶器凝成坯後、經二冷區拿拉坯機不進行連續切割的工藝。因鑄坯長度有一定限度,不能實現真正的連續澆鑄。一般只用於工業性試驗機,或用於鑄造帶承插口的...
半連續鑄錠時,金屬熔體被均勻地導入外壁用水冷卻的結晶器中,在結晶器壁和結晶器底座的共同作用下迅速凝固結晶,並形成一個較堅固的凝固殼。待結晶器中金屬熔體的...
上半連續分解空間(upper semi-continuous decomposition space)是一類拓撲空間。商空間是上半連續分解空間的充分必要條件是自然映射為閉映射。上半連續分解空間的概念是...
紡制粘膠長絲的方法之一。半連續式紡絲機的一面為凝固成形和拉伸部分,上部為水洗,另一面為離心罐受絲部分。經噴絲頭噴出的絲條經刮酸棒、拉伸盤,再繞至上下...
次線性函式(sublinear function)是一類重要的凸函式。正齊次且是次可加的函式稱為次線性函式。局部凸空間(包括賦范線性空間、有限維空間)上的下半連續次線性函式...
半連續矽熱法煉鎂(production of magne-sium by semicontinuous siliconthermic reduc-tivn)是指在真空電爐內,用矽鐵還原劑將煅燒白雲石還原成金屬鎂的熱還原法煉...
半連續式發酵法是指在主發酵階段採用連續發酵,而後發酵階段採用間歇發酵的方式。1、半連續式發酵法簡介在半連續發酵中,根據醪液的流加方式不同,又可分為兩種方法...
§20.單調函式的相對平均值 Ⅵ.習題 定義在任意集合上的數值函式 定義在拓撲空間上的數值函式 半連續數值函式 Stone.Weierstrass定理 定義在區間上的函式 凸函式 平...
