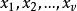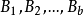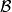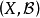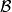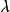簡介
區組設計是組合設計研究的主要對象之一。設有限集 X 含 v 個元素
,這些元素稱為點或處理。又設
是 X 的 b 個子集(其中可能有相同者),這些子集稱為區組,並將這些區組組成的子集族記為
。稱序偶
為一個區組設計。
當
中有一部分區組形成集 X 的一個劃分時,稱這部分區組為一個平行類。若可以劃分為若干個平行類,則稱該區組設計是可分解的。這樣定義的區組設計並不包含多少信息,為在理論研究和實際套用中得到有意義的對象,需要對區組設計加強條件。若每個區組的大小為k (< v),每個點在 r 個區組中出現,並且每兩個相異點恰同時出現在
個區組中,則稱這樣的區組設計為平衡不完全區組設計。
這一概念由
玻色(R.C.Bose) 於1939 年提出。在組合設計理論的發展過程中,平衡不完全區組設計受到了諸多形式的推廣,其中包括成對平衡設計,可分組設計,填充、覆蓋設計等。
套用
有關區組設計等基本問題之一是研究各種區組設計存在的充分必要條件。
20世紀60年代,哈納尼(H.Hanani)解決了當 k 值較小時這一類設計等存在性問題。
20世紀70年代,威爾遜(R.M. Wilson)提出了成對平衡設計閉集對概念並解決了對一般 k 值以及 v 充分大時這一類設計等存在性。
平衡不完全區組設計
平衡不完全區組設計(balanced incomplete block design),簡稱BIBD,是一類重要的區組設計。若 X 為 v 元點集,居為 X 的一些 k 元子集組成的族(這些 k 元子集稱為
區組),使得 X 中的任意點對恰好出現在幾個區組中,則稱區組設計為一個平衡不完全區組設計。
優點
(1)經濟性:
全部試驗水平可以不安排在同一個區組內進行,對區組的要求較低,經濟的解決了試驗成本。
(2)平衡性:
1)每個試驗水平重複次數相同(r相同);
2)每個區組包含的水平個數相同(k相同);
3)任意兩個水平對,在整個試驗中出現的重複次數相同(λ相同)。
(3)靈活性:
可以根據 k 的大小,靈活、分散的進行試驗。
(4)計算的嚴密性:
有嚴格的數學方法有效的消除系統誤差,故試驗精度高。
缺點
平衡不完全設計的缺點是:計算複雜。