在幾何學,某個曲線族的包絡線(Envelope),是跟該曲線族的每條線都有至少一點相切的一條曲線。(曲線族即一些曲線的無窮集,它們有一些特定的關係。)
基本介紹
- 中文名:包絡線
- 外文名:Envelope
- 套用學科:幾何學
- 公式:(A−s)x+sy= (A−s)(s)
- 定義:每條線有至少一點相切的一條曲線
- 相關術語:曲線族
幾何學定義


證明

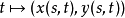





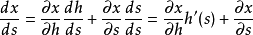




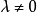

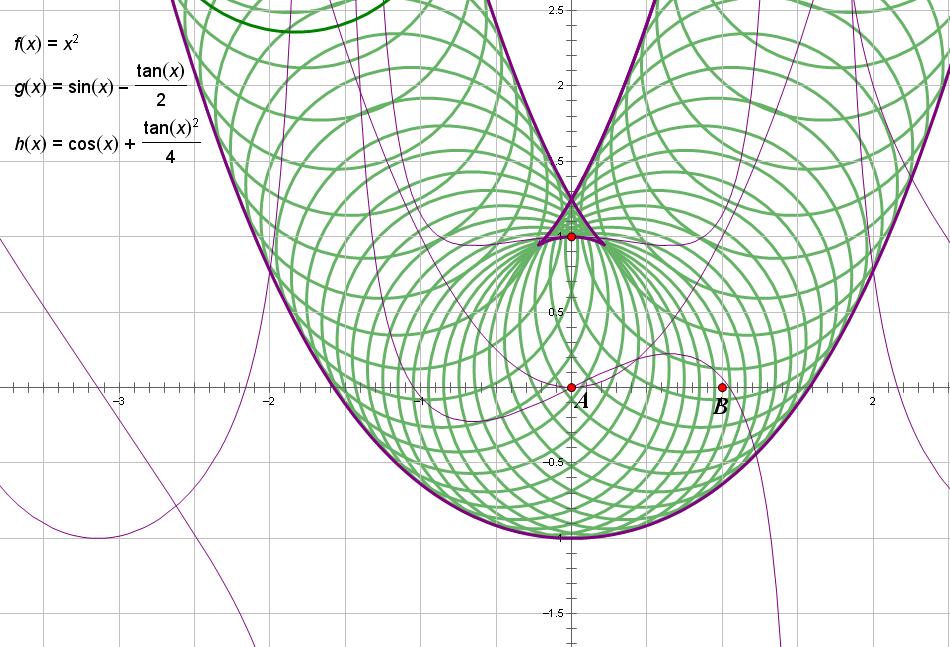
在幾何學,某個曲線族的包絡線(Envelope),是跟該曲線族的每條線都有至少一點相切的一條曲線。(曲線族即一些曲線的無窮集,它們有一些特定的關係。)



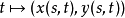





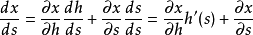




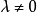

在幾何學,某個曲線族的包絡線(Envelope),是跟該曲線族的每條線都有至少一點相切的一條曲線。(曲線族即一些曲線的無窮集,它們有一些特定的關係。)...
包絡線法,envelopecurve technique,利用包絡線進行長期技術預測的方法。與幾條曲線相切並將其包絡起來的虛線,便是包絡線。...
包絡是由許多橢圓形曲線交織而成的一種圖形,外觀看起來是包起來的一樣。包絡在數學、信號處理、文學、經濟學、傳統中醫學上都有自己獨特的含義。...
應力包絡線又稱副載波包絡線(subcarrier envelope)。對基帶信號而言,有兩個載波,一個是光載波,另一個是射頻載波,...
包絡線被用來預測市場價格在平均價格上下波動的範圍,中軸為一條移動均線,將當前均線值加上或減去一個固定的百分比數額則可得到包絡線的上下軌。...
一個高頻調幅信號,它幅度是按低頻調製信號變化的。如果把高頻調幅信號的峰點連線起來,就可以得到一個與低頻調製信號相對應的曲線。這條曲線就是包絡線。 包絡指的...
若破壞包絡線為水平(平行於正應力軸),則莫爾圓上最大剪應力即屬作用在破壞面的剪應力。若破壞包絡線與水平軸成一角度,則破壞面上的剪應力小於莫爾圓的最大剪...
動態包絡線指的是軌道車輛(包括鐵路,捷運,輕軌,有軌電車等)通過懸掛系統連線在軌道上行駛時,其最大的縱向和橫向所占用空間的輪廓線。...
包絡函式(envelope function)是常見於電子工程領域,用來描述信號的一種特點。這種特點就是該信號的局部最大值的變化情況。...
中文名稱 包絡線機構 英文名稱 envelope mechanism 定義 組成高副的兩元素為一對互包絡曲線的平面高副機構。 套用學科 機械工程(一級學科),機構學(二級學科),...
振幅包絡線 Amplitude envelope 在振幅頻譜圖中,將各條譜線頂點連起來的曲線,稱振幅包絡線. ...
包絡是由許多橢圓形曲線交織而成的一種圖形,外觀看起來是包起來的一樣。包絡在數學、信號處理、文學、經濟學、傳統中醫學上都有自己獨特的含義。包絡環是研究無限...
頭廓包絡線是指不同百分位的駕駛員和乘員在乘坐狀態下,他們頭廓線的包絡線,用以確定車身內部頂棚的高度。將頭廓線樣板上的眼點沿著眼橢圓樣板上的上半部眼橢圓...
頻譜包絡是將不同頻率的振幅最高點連結起來形成的曲線,就叫頻譜包絡線。頻譜是許多不同頻率的集合,形成一個很寬的頻率範圍,不同的頻率其振幅可能不同。計算頻譜...
包絡檢波(envelope-demodulation)是基於濾波檢波的振動信號處理方法,尤其對初期故障和信噪比較低的故障信號識別能力強。將一段時間長度的高頻信號的峰值點連線,就可以...
包絡定理是在最大值函式與目標函式的關係中,我們看到,當給定參數 a 之後,目標函式中的選擇變數 x 可以任意取值。如果 x 恰好取到此時的最優值,則目標函式即與...
數據包絡分析方法(Data Envelopment Analysis,DEA)是運籌學、管理科學與數理經濟學交叉研究的一個新領域。它是根據多項投入指標和多項產出指標,利用線性規劃的方法,...
包絡解調又稱包絡檢波,適用於普通調幅信號的解調,指產生的輸出信號與已調信號包絡線成正比的幅度解調。...
數據包絡分析方法(Data Envelopment Analysis,DEA)是運籌學、管理科學與數理經濟學交叉研究的一個新領域。它是根據多項投入指標和多項產出指標,利用線性規劃的方法,...
摩爾包線指的是同一試樣在不同大小主應力達到極限狀態所得應力圓(即摩爾圓)的包絡線,該線上各點的坐標即表示剪下面上破壞時的法向應力與剪應力的組合。也叫...
漸屈線是曲線微分幾何中的概念,它是曲線上密切圓圓心的軌跡。等價的描述是一條曲線的漸屈線即是其法線的包絡。漸屈線與漸伸線是一對相對的概念,若曲線A是曲線...
