基本介紹
- 中文名:勒洛三角形
- 外文名:reuleaux triangle,curved edge triangle
- 也稱:魯洛三角形,萊洛三角形
- 發現者:勒洛
- 性質:定寬曲線和定寬性
- 套用:市政檢修井井蓋的形狀
- 又稱:魯洛三角形
定義
 勒洛三角形
勒洛三角形性質
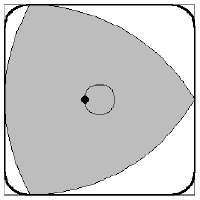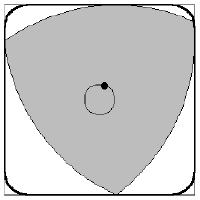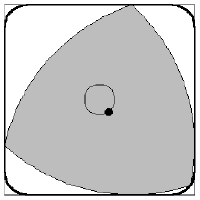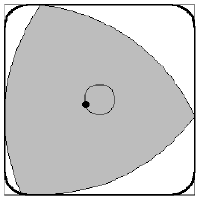

 轉子發動機
轉子發動機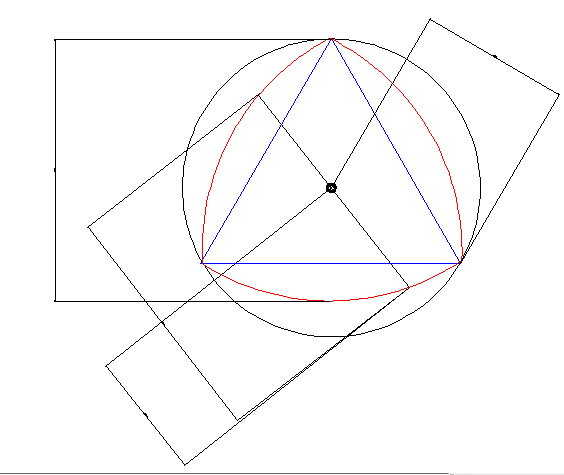
 勒洛三角形
勒洛三角形

 轉子發動機
轉子發動機勒洛三角形一種圖形。是以等邊三角形每個頂點為圓心,以邊長為半徑,在另兩個頂點間作一段弧,三段弧圍成的曲邊三角形就是勒洛三角形(reuleaux triangle ),也稱魯...
萊洛三角形,也譯作勒洛三角形或弧三角形、圓弧三角形,是除了圓形以外,最簡單易懂的勒洛多邊形,一個定寬曲線。...
魯洛克斯三角形(Reuleaux triangle)又稱“勒洛三角形”、“萊洛三角形”、“圓弧三角形”,是一種特殊三角形,指分別以正三角形的頂點為圓心,以其邊長為半徑作圓弧...
定寬曲線的概念指具有(類似圓的)定寬性的曲線。定寬曲線的舉例:圓形、勒洛三角形、月亮、圓球(太陽) 作一個等邊三角形ABC,然後以頂點A為圓心,三角形邊長為半徑...
9、萊洛三角形勒洛三角形是定寬曲線,用它來搬運東西,不會發生上下抖動青年問禪師:“大師,在單位,他們總嫌我稜角太突出,不合群!” 禪師掏出數根圓柱鋪在地上,...
禮花蛋每周推出一集:“長度單位史話”、 “機械運動”、 “摩擦力”、 “勒洛三角形”、 “神馬叫壓強”等等,每集三分鐘左右,能夠讓觀看者記住各個理科小知識...
46 勒洛三角形 15447 皮克定理 15748 莫雷定理 16049 雪花曲線 16350 謝爾賓斯基三角形 16651 超越極限 169附錄: 書中所提及定理的證明 173...
禮花蛋每周推出一集:“長度單位史話”、 “機械運動”、 “摩擦力”、 “勒洛三角形”、 “神馬叫壓強”等等,每集三分鐘左右,能夠讓觀看者在爆笑一刻的同時...
汪克爾發動機的基本結構是在一個橢圓形的空間中,置入一個勒洛三角形形狀的轉子,轉子的三個面將橢圓形空間劃分為三個獨立的燃燒室。由於轉子采偏心運轉,因此這些被...
禮花蛋每周推出一集:“長度單位史話”、“機械運動”、 “摩擦力”、“勒洛三角形”、 “神馬叫壓強”等等,每集三分鐘左右,能夠讓觀看者在爆笑一刻的同時輕鬆...
