萊洛三角形,也譯作勒洛三角形或弧三角形、圓弧三角形,是除了圓形以外,最簡單易懂的勒洛多邊形,一個定寬曲線。其作法為先畫正三角,然後分別以三個頂點為圓心,邊長長為半徑畫弧所得到的三角形。
基本介紹
- 中文名:萊洛三角形
- 別名:勒洛三角形,弧三角形
- 命名者:Franz Reuleaux
- 類型:曲邊三角形
做圖法,面積關係,性質,套用,
做圖法
弧三角形,又叫萊洛三角形, 是機械學家萊洛首先進行研究的.弧三角形是這樣畫的;先畫正三角,然後分別以三個頂點為圓心,邊長長為半徑畫弧得到的三角形。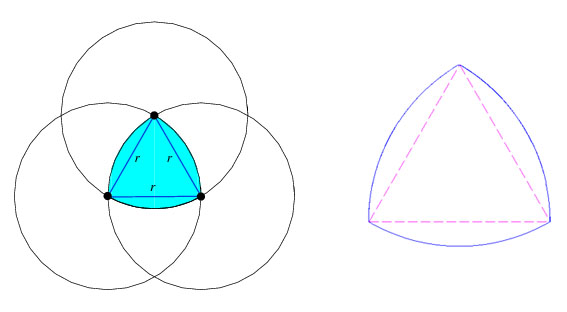 萊洛三角形畫法
萊洛三角形畫法
 萊洛三角形畫法
萊洛三角形畫法面積關係
性質
將一個曲線圖放在兩條平行線中間,使之與這兩平行線相切,則可以做到:無論這個曲線圖如何運動,只要它還是在這兩條平行線內,就始終與這兩條平行線相切,但中心點會形成一個圓。這個定義由Franz Reuleaux,一個十九世紀的德國工程師命名。 平行線的運動
平行線的運動
 平行線的運動
平行線的運動套用
1、萊洛三角形也是“除了圓形以外,還有什麼形狀的下水道蓋不會掉入下水道?”這個問題的一個答案。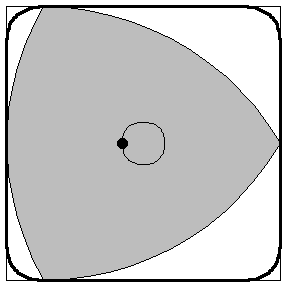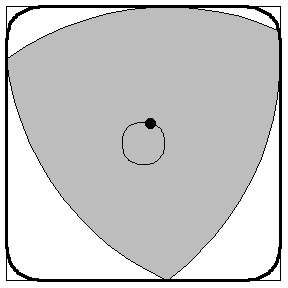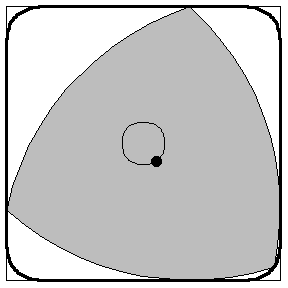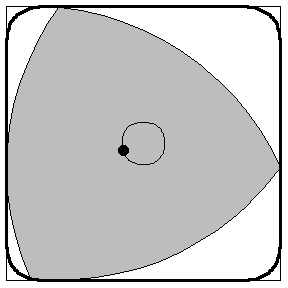 此類三角形旋轉
此類三角形旋轉
 此類三角形旋轉
此類三角形旋轉2、下圖為此類三角形旋轉的一個例子,因為這個特點,該類三角形可用於做運輸的輪子,搬東西穩定(但由於製作技術要求高,邊角不耐磨等原因不常用)。
還有一個用圓形而不用萊洛三角做輪子的原因:
用圓作車輪是人類文明發展過程中選擇的結果,不僅由於圓的定寬性,還由於圓是最常見的圖形之一,比如太陽,月亮等,也是所有定寬曲線中最簡單的。圓形較為容易加工。而且定寬的穩定性較好,即使圓形不算正規,還會保持較好的定寬性。
人們將車輪做成圓形,是利用了圓的一個重要性質:將一個圓放在兩條平行線中間,使之與這兩平行線相切。則可以做到:無論這個圓如何運動,它還是在這兩條平行線內,並且始終與這兩條平行線相切。此即圓的定寬性質,具有類似圓的定寬性質的曲線稱為定寬曲線。
另外,圓形還具有一條重要的性質,幾何中心的穩定性,圓的中軸(過圓心的軸)在圓轉動的時候是保持高度不變的,始終是地面往上半徑的高度。
試想用上面的萊洛三角形,它的幾何中心是不穩定的,隨著圖形的轉動上下跳動,這樣是不適合做車輪的。
基於抗訴特點,圓形的車輪是套用最廣泛的。
3、萊洛三角形形狀的鑽頭可鑽出四角為圓弧的正方形的孔。

