基本介紹
定義
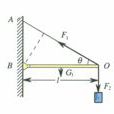
力距一般指本詞條




不等式左邊看成三點間的兩力距離之和,即意味著動點與定點與的距離之和,則由三角不等式可進行推證。...
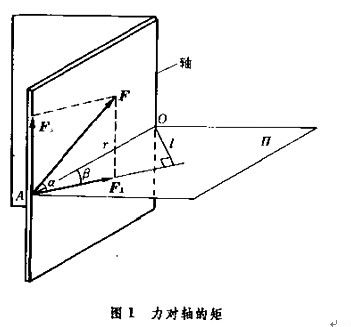
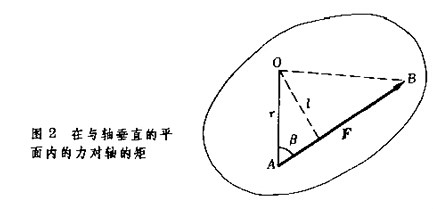
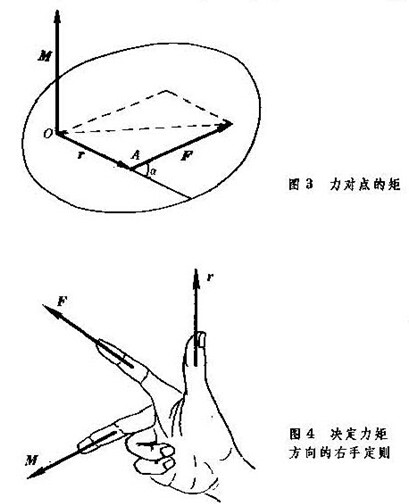
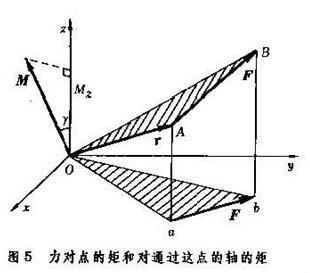
力矩(moment of force) 力對物體產生轉動作用的物理量。可以分為力對軸的矩和力對點的矩。即:M=LxF。其中L是從轉動軸到著力點的距離矢量,F是矢量力;力矩...
以軸流通風機玻璃鋼葉片為例,分析了葉片重量和重心距離偏差過大的原因,提出了...②由於合模間隙控制不當 (如中間夾布或緊固螺栓擰緊力不同等 ) 和氣袋充壓...
力偶是指兩個大小相等、方向相反,作用線平行但不共線的兩個力組成的力系, 力偶中兩個力之間的垂直距離d 稱為力偶臂。力偶中的力F與力偶臂d 的乘積稱為力偶...
特化了遠距離射擊戰的高達。Dynames高達的發展機,基本性能水漲船高,攻擊力以及命中精度均得以提高。進行遠距離射擊的狙擊模式時,在駕駛艙內展現射擊用的系統,駕駛...
步進電機轉速越高,力距越大則要求電機的電流越大,驅動電源的電壓越高。電壓對力矩影響如下:4、細分驅動器在步進電機步距角不能滿足使用的條件下,可採用細分驅動...
然而當飛機採用了推力矢量之後,發動機噴管上下偏轉,產生的推力不再通過飛機的重心,產生了繞飛機重心的俯仰力距,這時推力就發揮了和飛機操縱面一樣的作用。由於推力的...
在額定風速 (14m/s)以下時,通過調節發電機反力距使轉速跟隨風速變化,在高於額定風速時,通過變槳距系統使系統輸出功率穩定。所謂變槳距指安裝在輪載上的葉片通過...
在前一段時間,試驗中多次出現試樣斷在標距上或標距外(甚至在過渡部分)。...相關資料顯示,缺口的存在改變了試樣的受力條件,造成硬性的應力狀態,不利於材料...
無錫嵐凌卓維動力科技有限公司於2016年01月18日在無錫市新吳區市場監督管理局登記成立。法定代表人李敬美,公司經營範圍包括助力車中置電機、後驅電機、力距感測器...
(變壓) 調速電機,以嶄新調速原理獨特發明的永磁體低能耗變速方法(無需勵磁線圈及電氣控制器)均能達到無級調速,本發明電機具有雙頭出軸,B出軸為低調速輸出,力距...
