基本介紹
- 中文名:切割線定理
- 外文名:theorem of tangent and secant of a circle
- 所屬學科:數學(幾何學)
- 相關概念:切線,割線,弦切角定理等
基本介紹
切割線定理的證明
 圖1
圖1例題解析
 圖2
圖2



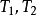










 圖3
圖3








 圖1
圖1 圖2
圖2













 圖3
圖3








切割線定理:從圓外一點引圓的切線和割線,切線長是這點到割線與圓交點的兩條線段長的比例中項。切割線定理的推論:從圓外一點引圓的兩條割線,這一點到每條...
一條直線與一條弧線有兩個公共點,我們就說這條直線是這條曲線的割線。 與割線有關的定理有:割線定理、切割線定理。常運用於有關於圓的題中。...
割線定理證明三 根據切割線定理求證。已知:從圓O外一點P引兩條圓的割線,一條交圓於A、B,另一條交圓於C、D求證:AP·BP=CP·DP...
於是相交弦定理、切割線定理、割線定理三者可以統一成下面的定理:設經過定點P的任何一條直線交圓O於兩點A、B,且圓O的半徑為r,則積PA·PB的值為丨丨op丨² ...
相交弦定理、切割線定理及割線定理(切割線定理推論)以及他們的推論統稱為圓冪定理。一般用於求線段長度。當P點在圓內時稱為相交弦定理,當P點在圓上時稱為切割線...
切割線(cross line):在航空物探測量中,由於受飛行高度、空間位置,以及儀器特性變化影響,各測線測量難以在同一水平,而且觀測誤差往往較大,因此需布設垂直於測線...
切割線定理:從圓外一點引圓的切線和割線,切線長是這點到割線與圓交點的兩條線段長的比例中項。推論:從圓外一點引圓的兩條割線,這一點到每條割線與圓的交點...
1 英文名稱 2 切線的判定和性質 ▪ 切線的判定定理 ▪ 切線的性質定理 3 切線長定理 4 弦切角定理 5 切割線定理 6 弦切角概念 弦...
圓冪定理是平面幾何中的一個定理,是相交弦定理、切割線定理及割線定理(切割線定理推論)的統一,例如如果交點為P的兩條相交直線與圓O相交於A、B與C、D,則PA·...
切割線定理割線定理相交弦定理圓冪定理西姆松定理托勒密定理蝴蝶定理婆羅摩笈多定理根心定理三圓定理四圓定理五圓定理坎迪定理三弦共點定理雞爪定理...
功能一全面囊括概念、公式、定理。1.收錄了國中數學、物理、化學三學科所涉及的...132切割線定理 從圓外一點引圓的切線和割線,切線長是這點到割 線與圓交點的...
圖Ⅱ:割線定理。如圖,連線AD、BC。可知∠B=∠D,又因為∠P為公共角,所以有,同上證得 。圖Ⅲ:切割線定理。如圖,連線AC、AD。∠PAC為切線PA與弦AC組成的...
切割線定理:從圓外一點引圓的切線和割線,切線長是這點到割線與圓交點的兩條線段長的比例中項。割線定理:從圓外一點P引兩條割線與圓分別交於A.B.C.D 則...
