定義
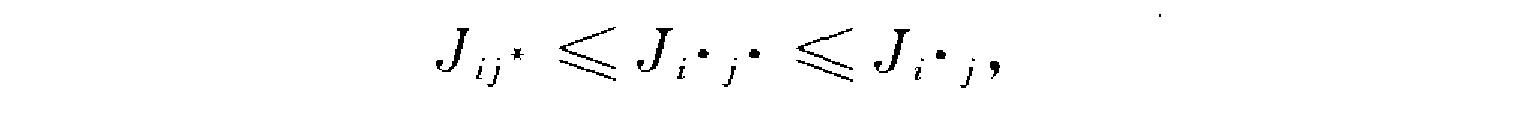
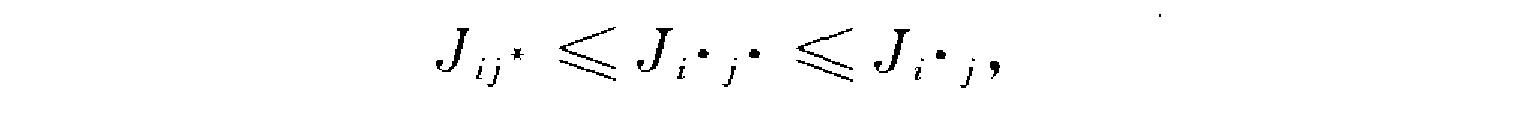
兩人零和對策(two person zero-sum game ) 一種最基本的完全對抗情形的對策模型.最初是由著名數學家約翰·馮·諾伊曼(John von Neuman)所提出,後來又由麻省理工...
兩人有限零和對策(two-person finite zero-sumgame)一類對策.指在一局對策中,只有兩個局中人,他們的策略都是有限的,他們的得失之和總為零.記為{S SZ;A},...
二人有限零和對策是兩個局中人都有有限個可供選擇並能作出最優決策的策略。這種策略付諸實施的結果是產生平衡局勢,即參與對策的兩個局中人在更換掉原先選定的策略...
動態兩人零和對策(dynamic two-person zero-sum game)一種微分對策.指微分對策問題中對抗雙方得失相抵,其和為零的對策.在定量微分對策中,參與對策的雙方具有相同...
什麼是零和對策 這一概念最初是由著名數學家約翰·馮·諾伊曼(John von Neuman)所提出,後來又由麻省理工學院的經濟學家萊斯特·瑟羅(Lester Thurow)加以推廣。零...
非零和對策是一類非完全對抗的對策問題,局中人之贏得總和不恆為零(或任何一個常值)的對策問題。由於這時既可能通過協商、合作增加總的收益,導致各人均有所得,...
在有限二人零和對策中,稱存在鞍點的對策為嚴格決定了的對策(稱矩陣遊戲更妥當),簡稱嚴格決定對策(strictly determined game),有些對策沒有鞍點,有些則有許多鞍點。...
競爭型決策是有關競爭對手之間的決策方法。決策者在競爭場合下作出的決策,或者說競爭的各方為了自己獲勝採取的對付對方的策略,一般稱為對策,研究它的理論和方法,稱...
第12章 二人有限非零和對策12.1 二人有限非零和對策問題12.2 非合作的二人有限非零和對策12.3 合作的二人有限非零和對策習題12...
16.3 簡化為對策的解 16.4 一般線性規劃和它的對偶 16.5 一般線性規劃和兩人零和對策的等價 16.6 為計算而安排的線性規劃 16.7 凸集的一些性質 16.8 解...
7.3.2 矩陣對策(兩人有限零和對策)的純策略(176) 7.3.3 矩陣對策的混合策略(179) 7.4 求解矩陣對策的方法(183) 7.4.1 圖解法(183) 7.4.2 線性規劃...
7.2.2 矩陣對策(兩人有限零和對策)的純策略 156 7.2.3 矩陣對策的混合策略 159 7.3 求解矩陣對策的方法 164 7.3.1 圖解法 164 7.3.2 線性規劃法 16...
博奕理論,又稱“對策論”或“遊戲理論”Gamethorey。西方國際關係理論中科學行為主義流派的一種研究理論和研究方法。它原本是數學運籌學中的一個支系,用於嚴格地處理...
排隊論、模擬理論、計畫評審與技術、圖和網路、規劃問題、決策分析、對策論等...第3節兩人非零和對策和n人對策372第4節案例題378第5節練習題383...
7.2.2 矩陣對策(兩人有限零和對策)的純策略7.2.3 矩陣對策的混合策略7.3 求解矩陣對策的方法7.3.1 圖解法7.3.2 線性規劃法...
5.3兩人非零和對策及n人對策5.4承包工程的投標報價策略第6章 項目評估直接法6.1概述6.2專家評價法6.3特爾斐(Delphi)方法6.4穆迪順序圖...
競爭性決策是參加競爭的各方在考慮對方可能採用某種策略的基礎上選擇最優對策的過程。競爭包括對抗性和非對抗性競爭、合作或協商。...
