以俄國學者克拉索夫斯基命名的一種構造李雅普諾夫函式,判定非線性控制系統穩定性的方法。
基本介紹
- 中文名:克拉索夫斯基方法
- 外文名:Krasovskii method
- 學科:電力科學
- 拼音:kè lā suǒ fū sī jī fāng fǎ
釋義
推導過程
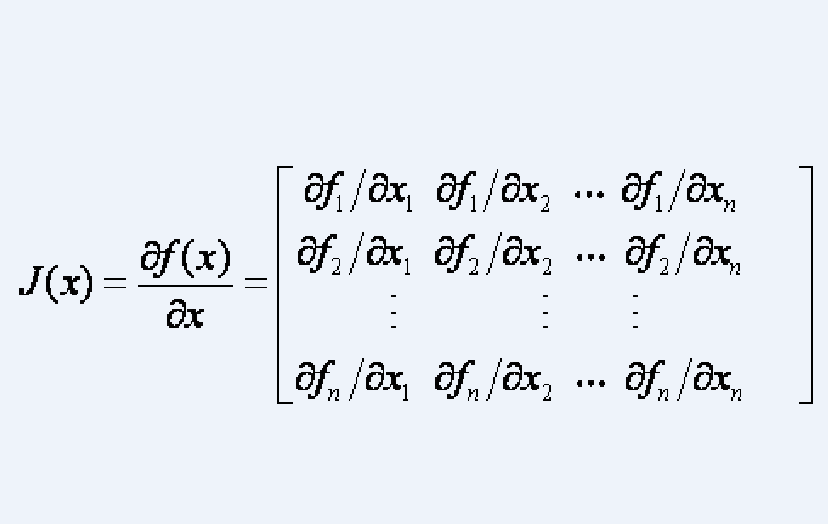
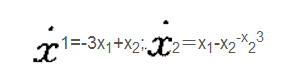
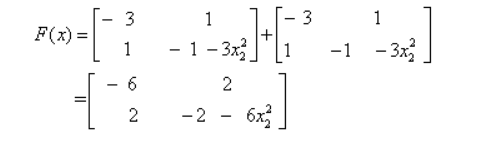

以俄國學者克拉索夫斯基命名的一種構造李雅普諾夫函式,判定非線性控制系統穩定性的方法。
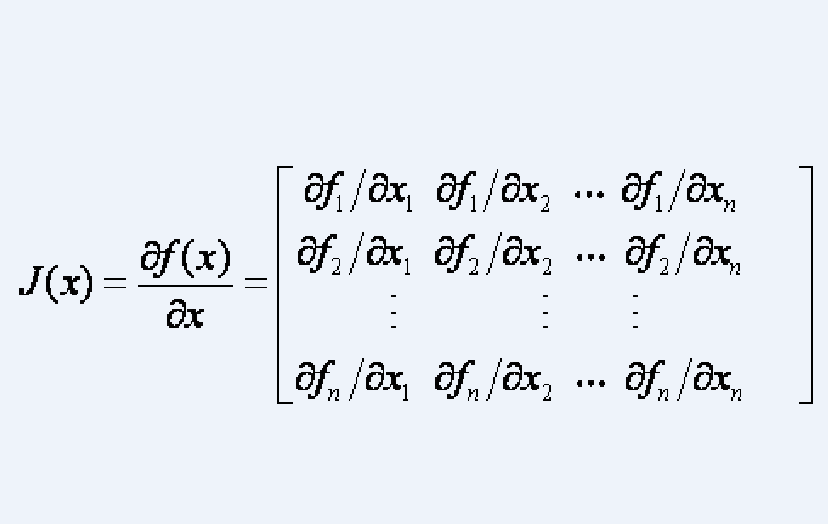
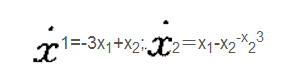
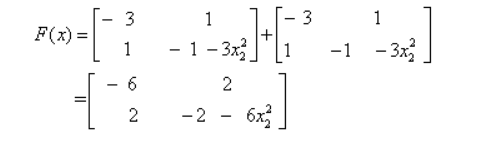
以俄國學者克拉索夫斯基命名的一種構造李雅普諾夫函式,判定非線性控制系統穩定性的方法。釋義以俄國學者克拉索夫斯基命名的一種構造李雅普諾夫函式,判定非線性控制系統穩定性的方法。推導過程考慮非線性系統x=f(x);f(0)=0...
同樣也可以用來解決控制受限下的能控域的結構問題.1938年,蘇聯數學家克列因(LpeHH, M.I'.)首先對L矩量論問題作了詳細的討論.1957年,蘇聯學者克拉索夫斯基(Ipacoacxuh, H. H.)利用這個方法求定常連續線性系統的快速控制,其...
李亞普諾夫泛函方法是李亞普諾夫第二方法對泛函微分方程的一種推廣。克拉索夫斯基於1959年提出了在空間C中解釋軌線的觀點,同時引入李亞普諾夫泛函V(t,φ)的概念。簡介 李亞普諾夫泛函方法是李亞普諾夫第二方法對泛函微分方程的一種推廣...
1936年推導出地球橢球的參數;1941年在他的指導下又推出地球橢球的新的參數,1946年蘇聯部長會議批准將它作為蘇聯的參考橢球,稱為“克拉索夫斯基橢球”。在此期間,又建議在布置天文大地網的同時應進行全面的重力測量,推動了蘇聯的大地重...
安東·克拉索夫斯基,今日俄羅斯前主持人。人物經歷 2023年2月,克拉索夫斯基在未出庭的情況下被烏克蘭法院判處五年監禁。烏克蘭國家安全局稱,克拉索夫斯基被控犯有兩項罪名,一項是煽動種族滅絕,另一項是鼓吹推翻烏克蘭憲法體系。2023年...
克拉索夫斯基環形山(Krasovskiy)是月球背面赤道區中的一座大型撞擊坑,約形成於晚雨海世,其名稱取自蘇聯天文學家及大地測量專家費奧多西·尼古拉耶維奇·克拉索夫斯基(Feodosiy Nikolaevich. Krasovskiy,1878年–1948年),1970年被...
《大地坐標計算用表(克拉索夫斯基橢圓體)》是現代蘇聯測繪總局編著的工具書。內容簡介 《大地坐標計算用表(克拉索夫斯基橢圓體)》全書22.5萬字。緯度範圍3°—56°。原表中第Ⅱ表系緯度80°一90°的數據未列入。
阿列克西·克拉索夫斯基(Oleksii Krasovskyi),男,1994年3月30日出生,烏克蘭越野滑雪運動員。2022年,代表烏克蘭參加2022年北京冬季奧運會。早年經歷 阿列克西·克拉索夫斯基,八歲時在烏克蘭肖斯特卡開始參加越野滑雪運動。職業生涯 2022...
只限於認定是C→Rⁿ。1959年,克拉索夫斯基(Н.Н.Красовский)提出把軌線段 視為空間 的元,把解映射T(t,σ):C→C定義為T(t,σ)φ=xₜ(σ,φ),於是滯後型泛函微分方程可寫成 其中 是右導數,...
我國於20世紀50年代,採用參心坐標系、克拉索夫斯基橢球參數建立了國家大地坐標系統—1954年北京坐標系。1980西安坐標系是我國於20世紀80年代採用參心坐標系、IAG-75橢球參數建立的國家大地坐標系統。隨著社會的進步,國民經濟建設、國防建設...
5.3.4克拉索夫斯基方法 5.4線性系統的Lyapunov穩定性分析 5.4.1連續系統的Lyapunov穩定性分析 5.4.2離散系統的Lyapunov穩定性分析 5.5MATLAB線上性系統穩定性分析中的套用 5.5.1Lyapunov第一法 5.5.2Lyapunov第二法 5.5.3...
10.4構造李亞普諾夫函式的一些方法 10.4.1克拉索夫斯基方法 10.4.2變數梯度法 10.5小結 習題 第十一章 非線性控制系統 11.1引言 11.2相平面法的概念 11.2.1相平面、相軌跡和相平面圖 11.2.2相軌跡的性質 11.3相平面圖...
5.6.1克拉索夫斯基法 5.6.2阿塞爾曼法 5.7基於Lyaponov第二法的參數最優問題 5.7.1線性二次型最優控制問題 5.7.2參數最優問題的Lyaponov第二法的解法 5.8基於Lyaponov第二法的模型參考控制系統 5.8.1模型參考控制系統...
10.4.1 克拉索夫斯基方法 10.4.2 變數梯度法 10.5 非線性系統校正與利用非線性特性改善控制系統性能 10.5.1 非線性系統校正 10.5.2 利用非線性特性改善控制系統性能 小結 典型例題分析 習題 附錄A 線性代數概述 附錄B ...
6.6.1 克拉索夫斯基法 (178)6.6.2 變數梯度法 (180)6.7 利用MATLAB分析系統的穩定 (182)6.7.1 利用李亞普諾夫第一法判斷系統的穩定性 (182)6.7.2 利用李亞普諾夫第二法判斷系統的穩定性 (183)思考題與習題 (...
5.4構造李雅普諾夫函式的規則化方法 5.4.1變數梯度法 5.4.2克拉索夫斯基方法 5.5連續時間線性系統的狀態運動穩定性判據 5.5.1線性時不變系統的穩定判據 5.5.2線性時變系統的穩定判據 5.6連續時間線性時不變系統穩定自由運動...
5.5.1 克拉索夫斯基法 182 5.5.2 變數梯度法 184 5.6 套用MATLAB分析線性系統穩定性 187 5.6.1 MATLAB函式簡介 187 5.6.2 MATLAB仿真實例 187 習題 191 第6章 線性系統的綜合 193 6.1 狀態反饋與極點配置 ...
5.4 李雅普諾夫函式的常用構造方法 167 5.4.1 變數梯度法 167 5.4.2 克拉索夫斯基方法 170 5.5 線性系統的狀態運動穩定性判據 171 5.5.1 線性定常系統狀態運動的穩定性判據 171 5.5.2 線性時變系統平衡狀態的穩定性判據 ...
11.5李雅普諾夫方法在非線性系統中的套用 11.5.1克拉索夫斯基方法 11.5.2變數梯度法 11.6小結 第12章最優控制 12.1引言 12.2最優控制問題 12.2.1幾個示例 12.2.2最優控制問題的數學描述 12.3泛函和變分法 12.3.1...
6.2 李亞普諾夫穩定性理論 6.2.1 平衡狀態 6.2.2 李亞普諾夫穩定性定義 6.2.3 李亞普諾夫第二法的主要定理 6.3 構造李亞普諾夫函式的規則化方法 6.3.1 克拉索夫斯基方法 6.3.2 變數梯度法 6.4 線性連續時間系統的零...
7.3.4非線性系統的李雅普諾夫穩定性分析克拉索夫斯基法 7.3.5李雅普諾夫第二法的其他套用 7.4控制系統的能控性和能觀測性 7.4.1能控性和能觀測性的定義 7.4.2線性定常連續系統的能控性判據 7.4.3線性定常連續系統的...
9.4.1克拉索夫斯基法 9.4.2變數梯度法 習題 第十章控制系統的狀態空間設計法 10.1線性系統的狀態反饋控制 10.1.1狀態反饋和輸出反饋的構成特點 10.1.2狀態反饋系統和輸出反饋系統的能控性和能觀性 10.1.3狀態反饋系統的極點...
是全局漸近穩定的,李亞普諾夫(А.М.Ляпунов,)原來只考慮原點附近即局部的穩定性,克拉索夫斯基(Н.Н.Красовский)將其推廣為全相空間,即全局的穩定性。相關概念定理 平衡狀態 考慮如下非線性動態系統(可以是...
1907年,德國赫爾默特用重力測量方法求得橢球長半徑為6378200m、扁率為1∶298.3。1910年,美國海福特根據重力測量結果推算橢球長半徑為6378388m、扁率為1∶297.0;1924年國際大地測量學會推薦為國際橢球。1940年蘇聯克拉索夫斯基利用更多...
在這前後,1901年的赫爾默特(Helmert)、1928年的海斯坎寧(Heiskanen)、1938年的克拉索夫斯基(Krassovsky)和1948年的傑弗瑞斯,所得數值都非常接近予海福德的結果。到最近二、三十年,由人造衛星軌道確定的地球扁率,其精度要比天文...
蘇聯的天文重力水準工作開始於上世紀三十年代,即莫洛金斯基提出這個方法之後。利用蘇聯擺儀全盤重力測量資料按天文重力水準方法求得的似大地水準面高度,曾用於推求克拉索夫斯基橢球的最適合的大地測量起始數據,以後在蘇聯天文大地網的整體...
6.3.1 李雅普諾夫第一方法 6.3.2 李雅普諾夫第二方法 6.4 李雅普諾夫方法線上性系統中的套用 6.5 李雅普諾夫方法在非線性系統中的套用 6.5.1 克拉索夫斯基判別法 6.5.2 變數梯度法 6.6 外部穩定性和內部穩定性 6.6...
我國的1954年北京坐標系採用克拉索夫斯基橢球,大地原點當是1942年大地坐標系原點。1954年北京坐標系建立之初,我國三角點的高程異常值由前蘇聯一等三角鎖9個基線網的18點已有的高程異常值為已知,按天文水準方法推算。此後,在1954年前...
為防止磁場畸變,對於1:100萬或1:50萬比例尺測量數據,採用了逐級縮小格線間距的方法。本航磁圖採用雙標準緯線等角圓錐投影,使用克拉索夫斯基1940橢球,中央經線110°E,南標準緯線25°N,北標準緯線47°N。
