基本介紹
- 中文名:天文重力水準
- 外文名:astro-gravimetric leveling
- 作用:推算相鄰點的大地水準面高差
- 數據來源:天文大地垂線偏差和重力測量數據
- 一級學科:工程技術
- 二級學科:測繪科學
發展歷史
計算
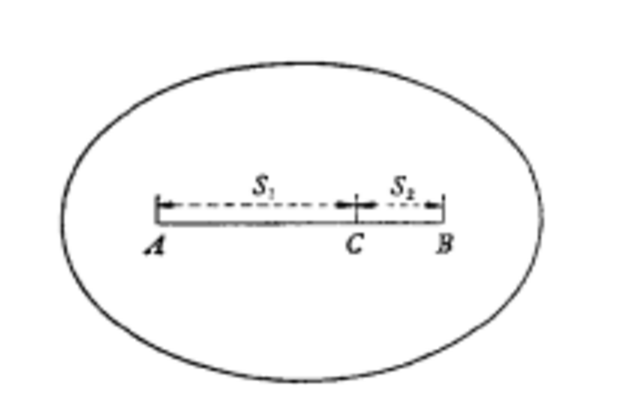 圖1
圖1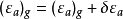
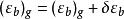
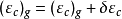
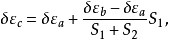
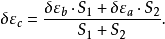
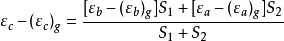
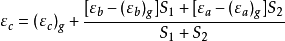
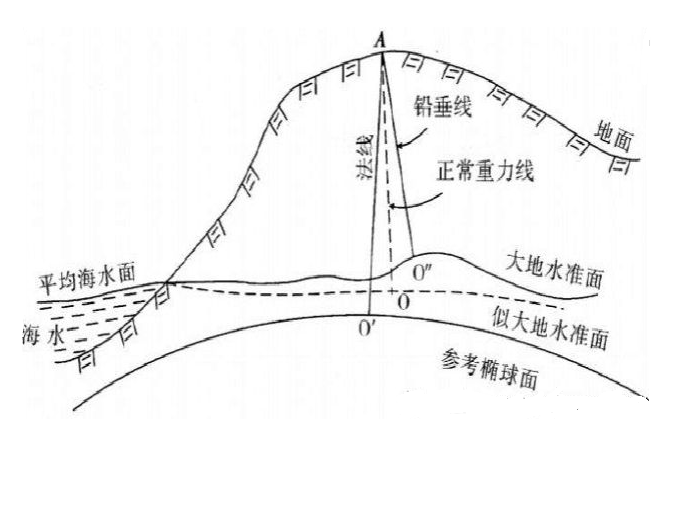
 圖1
圖1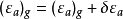
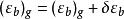
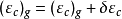
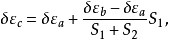
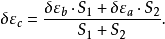
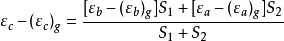
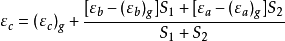
天文重力水準(astro-gravimetric leveling)是利用天文大地垂線偏差和重力測量數據,推算相鄰兩點的大地水準面差距之差(高差或高程異常差)的方法。當兩天文點的距離較遠...
天文水準(astronomical leveling)是指用天文大地垂線偏差推算兩點間的大地水準面高差或高程異常差的方法。當兩天文點相距不遠,垂線偏差呈線性變化時,利用兩點的天文...
一種綜合利用天文大地測量和重力測量數據計算相對大地水準面差距的方法。它是在兩已知天文大地點A、B相距較遠(例如幾十公里到百餘公里)的情況下,利用此兩點周圍...
亦可根據全球重力數據按斯托克斯(G·G·Stokes)公式計算;②相對大地水準面差距,是大地水準面沿法線到參考橢球面的距離,可用天文水準測量或天文重力水準測量方法求得,...
垂線偏差對於大地控制網的尺度控制也有一定的作用,因為利用垂線偏差由天文水準或天文重力水準求得的大地水準面至橢球面的差距若有6.38 m的誤差,地面上起始邊化算到...
他從事近代地球外部重力場逼近理論研究,建立了高逼近級的高程異常和垂線偏差統一逼近模型理論,提出地球外部重力場的虛擬單層密度表示方法。開展國家天文重力水準及航天...
地麵點沿鉛垂線到似大地水準面的距離稱為正常高,以似大地水準面定義的高程系統成為正常高系統。正常高與正高的差值與正常重力等參數有一定關係。正高系統中待定點...
此後,在1954年前蘇聯中央測繪科學研究所又重新進行了其國內的天文重力水準路線平差,也由於又重新計算了我國測定的一些天文點經度和測定了某些新的天文點等原因,於是...
長期從事物理大地測量理論和方法的研究,從50年代至70年代,他主要研究我國天文重力水準的理論、方法和精度,其研究成果完善了當時由蘇聯專家為我國設計的天文重力水準...
1957年,主持全國天文重力水準網和重力基本網的測量規劃,提出方格模板計算方案,被蘇聯、東歐和中國的教科書稱為“方俊方格模板法”。 [1] ...
我國精密重力的相對聯測 精密重力測量的潮汐改正 天文重力水準計算公式的改化 利用局部重力資料改善高階地球重力場模型 區域高階重力場模型與青藏地區局部位系...
·研究月球及太陽系行星的形狀及其重力場。建立和維持具有高科技水平的國家和全球的天文大地水平控制網和精密水準網以及海洋大地控制網,以滿足國民經濟和國防建設的...
這兩者都可通過天文水準或天文重力水準的方法求定。由圖可知:H大=H正+NH大=H常+ξ於是,大地高H大同正高H正或同正常高H常之間通過N或ξ聯繫了起來而可互相...
似大地水準面至橢球面的距離。它分為重力高程異常和天文大地高程異常。前者是似大地水準面到正常橢球面的距離,可利用地面上的重力異常計算求得。後者是似大地水準面...
本書系統地論述了物理大地測量學的基礎知識,包括斯托克司邊值理論、莫洛金斯基邊值理論、地球形狀和外部重力場的實際確定、確定大地水準面高和高程異常的天文大地...
6.2.1根據任務的需要,收集測區範圍既有的國家三角點、導線點、天文重力水準點、水準點、甚長基線干涉測量站、衛星雷射測量站、天文台和已有的GPS站點資料,包括點...
傳統求定高程異常ξ值的方法是外業獲取的大地測量工作者沿著一等三角鎖段布設天文重力水準路線,利用天文重力水準的方法計算出高程異常ξ,再利用水準聯測三角點,求...
定位採用的橢球體面與我國大地水準面符合較好;天文大地坐標網傳算誤差和天文重力水準路線傳算誤差都不太大;天文大地坐標網的坐標經過了全國性整體平差,坐標統一,...
隨後在蘇聯中央測繪科學研究所工作,從事地球形狀和地球重力場的研究。1945年他發表了《大地重力學的基本問題》一文,還提出天文重力水準方法。從此,在國家控制網中...
包括三角測量、導線測量、水準測量、天文測 量、重力測量、慣性測量、橢球面大地測量、地球形 狀理論和測量平差計算;②衛星大地測量學。它是采 用在地面上測定宇宙...
寧津生教授是中國著名的大地測量學家,長期從事物理大地測量理論和方法的研究,從50年代至70年代,他主要研究我國天文重力水準的理論、方法和精度,其研究成果完善了當時...
據2016年12月研究所官網顯示,研究所發起並參與完成了第一代國家重力網和國家天文大地網及國家天文重力水準網、國家天文基本點網的建設,為中國第一顆人造衛星上天、...
前者包括高精度重複水準測量、天文測量、重力測量等,後者包括甚長基線干涉測量、衛星雷射測距、衛星都卜勒定位和GPS衛星定位、衛星雷達測高、衛星跟蹤技術等。...
