克拉索夫斯基橢球是克拉索夫斯基於1940年提出的地球橢球,其長半徑為6378245米,短半徑為6356863米,扁率為1/298.3。
基本介紹
- 中文名:克拉索夫斯基橢球
- 外文名:Krassovsky ellipsoid
- 提出者:克拉索夫斯基
- 適用領域:測繪學
作者介紹
地球橢球的基本幾何參數




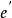
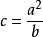




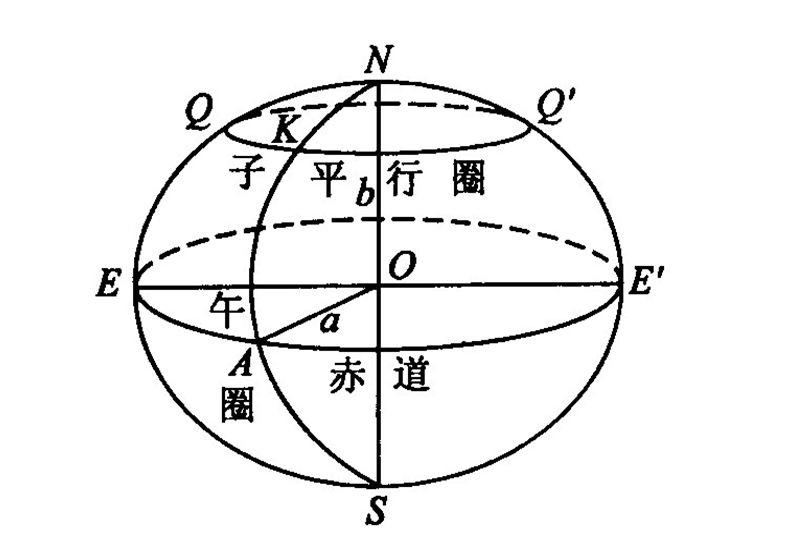
克拉索夫斯基橢球是克拉索夫斯基於1940年提出的地球橢球,其長半徑為6378245米,短半徑為6356863米,扁率為1/298.3。




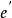
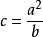




克拉索夫斯基橢球是克拉索夫斯基於1940年提出的地球橢球,其長半徑為6378245米,短半徑為6356863米,扁率為1/298.3。...
克拉索夫斯基(Krasovski,Kheodosi Nikolaevich,1878~1948)蘇聯數學家、大地測量學家。蘇聯科學院通訊院士。1878年9月26日生於俄國科斯特羅馬州加利奇城,1948年10...
我國1952年以前採用海福特橢球(該橢球1924年被定為國際橢球),從1953年起,開始改用克拉索夫斯基橢球。1978年我國決定採用國際大地測量協會所推薦的"1975年基本大地...
大陸地區在1954年前曾採用International 1924參考橢球,之後較長一段時間內採用基於克拉索夫斯基(Krasovsky)1940的1954年北京坐標系。1980年開始使用1975年國際大地測量與...
1940年蘇聯克拉索夫斯基利用更多的弧度測量和重力測量資料,求得橢球長半徑為6378245m、扁率為1∶298.3。1978年,中國根據弧度測量和重力測量資料,推算的橢球長半徑為...
北京54坐標系(BJZ54)是指北京54坐標係為參心大地坐標系,大地上的一點可用經度L54、緯度M54和大地高H54定位,它是以克拉索夫斯基橢球為基礎,經局部平差後產生的...
54坐標係為參心大地坐標系,大地上的一點可用經度L54、緯度M54和大地高H54定位,它是以克拉索夫斯基橢球為基礎,經局部平差後產生的坐標系。...
“1954年北京坐標系”,是採用蘇聯克拉索夫斯基橢圓體,在1954年完成測定工作的,所以叫“1954年北京坐標系”,我國地形圖上的平面坐標位置都是以這個數據為基準推算...
北京54坐標系(BJZ54)是指北京54坐標係為參心大地坐標系,大地上的一點可用經度L54、緯度M54和大地高H54定位,它是以克拉索夫斯基橢球為基礎,經局部平差後產生的...
莫洛金斯基證明;為了滿足似大地水準面相對於克拉索夫斯基橢球之高度的要求,必須提高精度,即似大地水準面高度的均方誤差不得大於±3米。根據他的建議開始布設許多...
54坐標系採用的是克拉索夫斯基橢球體。該橢球在計算和定位的過程中,沒有採用中國的數據,該系統在中國範圍內符合得不好,不能滿足高精度定位以及地球科學、空間科學...
這一方法成功地被用於推算地球橢球,如著名的海福德橢球和克拉索夫斯基橢球都是採用這一方法推算出來的。 為了推求地球扁率,赫爾默特由月球黃緯、黃經的運動推算出...
(1)橢球參數與克拉索夫斯基橢球相比精度高。(2)橢球有4個參數,是一套完整的數值,既確定了幾何形狀,又表明了地球的基本物理特徵,從而將大地測量學與大地重力學的...
釋文:新1954年北京大地坐標系是將1980年國家大地坐標系下的全國天文大地網整體平差成果,以克拉索夫斯基橢球體面為參考面,通過坐標轉換整體換算至1954年北京坐標系下...
54坐標系採用的是克拉索夫斯基橢球體。該橢球在計算和定位的過程中,沒有採用中國的數據,該系統在中國範圍內符合得不好,不能滿足高精度定位以及地球科學、空間科學...
大地坐標(Geodetic coordinate)是大地測量中以參考橢球面為基準面的坐標,地麵點P...屬於參心大地坐標系,採用了前蘇聯的克拉索夫斯基橢球體。其長半軸a=6378245,...
其坐標原點不在北京,而在俄羅斯的普爾科沃,參考橢球為克拉索夫斯基橢球。 [1] 參考資料 1. http://www.gsdkj.net/pro/view.php?id=356 詞條標籤: 地理, ...
