基本介紹
- 中文名:修正劍橋模型
- 外文名:Modified Cambridge model
- 提出者:羅斯科、伯蘭特
- 主要修正內容:屈服面形狀
- 提出時間:1968年
- 學科:土力學
產生及推導
劍橋模型
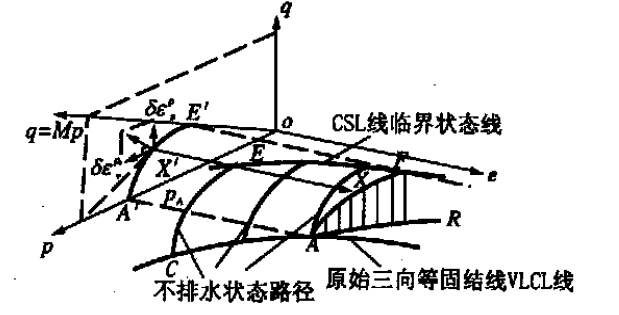 圖1 劍橋模型示意圖
圖1 劍橋模型示意圖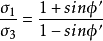
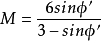
修正劍橋模型的推導
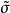
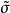
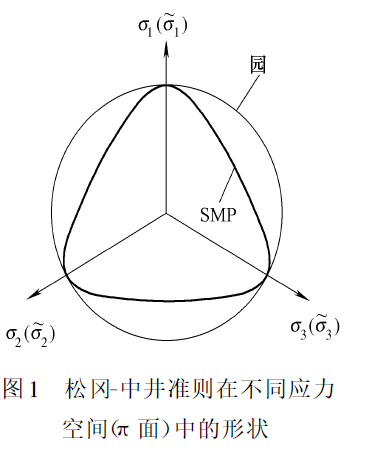 圖2
圖2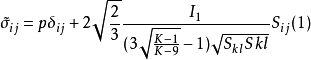
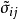
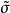
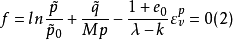
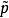
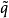
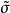
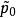
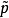
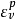
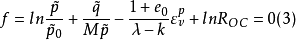
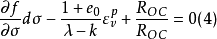

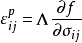
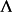
 圖1 劍橋模型示意圖
圖1 劍橋模型示意圖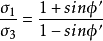
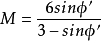
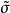
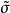
 圖2
圖2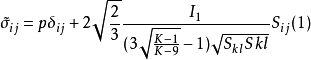
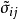
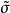
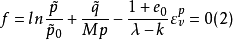
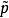
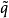
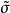
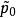
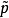
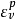
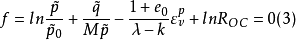
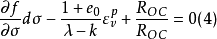

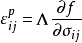
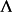
羅斯科(Roscoe)和伯蘭特(Burland)於1968年對劍橋模型作了修正後提出的一個土的彈塑性模型。主要是對劍橋模型的彈頭形屈服面形狀作了修正,認為屈服面軌跡應為橢圓。...
劍橋模型是指由英國劍橋大學Roscoe等於1963年提出的,這個模型基於正常固結土和超固結土試樣的排水和不排水三軸實驗基礎上,提出了土體臨界狀態的概念,並在實驗基礎上...
建立在彈塑性模型理論基礎上的一類本構模型。已經建立的彈塑性模型很多,影響較大的有: 劍橋模型;修正劍橋模型;拉特-鄧肯模型;邊界面模型;清華彈塑性模型、沈珠江三...
魏汝龍-Khosla-Wu模型是一種土的土的臨界狀態模型,魏汝龍、Khosla、Wu等人依據修正劍橋模型的屈服面形狀為通過坐標原點的橢圓,根據正常固結粘土不排水三軸壓縮試驗的...
MARC包含一個土工模組,可以求解比奧固結方程,其材料庫中有修正劍橋模型等。清華大學水利水電工程系利用該軟體已完成不少工程和科研項目。在大型有限元軟體MARC中添加...
臨界狀態彈塑性模型是指建立在臨界狀態邊界面概念上的模型。英國劍橋大學羅斯科等於1958~1963年在正常固結土和弱超固結土的三軸剪下試驗的基礎上,發展了倫杜列克在...
[33] 原狀土的劍橋模型和修正劍橋模型[J].岩土力學, 2015, 36(s2): 215-220.[32] 考慮原狀土初始應力狀態的修正SMP屈服準則[J].水文地質工程地質, 2015,...
[3] 孔亮,惠治鑫,王燕昌.旋轉運動硬化理論與統一硬化參量在修正劍橋模型中的套用[J].寧夏大學學報(自然科學版),2008,29(2):139-143...
6.5.2 劍橋模型(彈塑性帽子模型)6.5.3 修正的劍橋模型6.5.4 基於修正劍橋模型的應力一應變關係工程材料的本構演繹附錄 固體力學問題的張量表述...
5.4 彈塑性本構模型通析5.5 分析預測5.6 土性指標5.7 狀態面5.8 本章小結第6章 土的硬化參量構成6.1 硬化參量的概念6.2 修正劍橋模型的硬化參量...
7.3.2修正劍橋模型 7.3.3有限元程式 7.4小結 參考文獻 8土工原位測試 8.1概述 8.1.1旁壓測試原理 8.1.2旁壓儀種類 8.1.3錐形貫入測試 ...
張雲. 修正劍橋模型參數對計算結果的影響 [21] [J]. 岩土力學,2006,03:441-444.張雲,薛禹群,吳吉春,李勤奮. 抽灌水條件下上海砂土層的變形特徵和變形參數 [22...
8、范慶來,欒茂田,楊慶.修正劍橋模型的隱式積分算法在ABAQUS中的數值實施.岩土力學, 2008, 29(1).9、欒茂田,范慶來,楊慶.非均質軟土地基上吸力式沉箱抗拔承載...
路德春以劍橋模型和修正劍橋模型為基礎,利用插值法理論上得出了可以反映土體欠固結程度的彈塑性本構模型[1] 。欠固結粘土循環荷載下軟粘土動力特性研究 編輯 關於...
20 惠治鑫 旋轉運動硬化理論與統一硬化參量在修正劍橋模型中的套用 寧夏大學學報 2008.2 21 伏振興 二能級系統中粒子布居振盪的布洛赫矢量分析 北京聯合大學學報...
建立了66個考慮土體、基坑支護體系和隧道結構模型共同作用的三維有限元模型,土體採用修正劍橋模型,分別研究了基坑坑底淺部土體加固、隧道兩側土體加固、基坑外圍周邊...
本構模型:線彈性模型、莫爾庫侖模型、土體硬化模型、小應變土體硬化模型、軟土蠕變模型、軟土模型、修正劍橋模型、霍克-布朗模型、節理岩體模型、NGI-ADP模型、...
4.1 利用修正劍橋模型描述土的回響4.2 擾動狀態理論導入平衡方程4.3 滲流連續方程4.4 綜合方程4.5 有限元程式編制4.6 算例本章小結參考文獻...
20.3.1採用修正劍橋模型模擬軟粘土地層應力應變特性20.3.2流固耦合模擬隧道開挖地層變形時效性20.3.3殼單元模擬隧道襯砌支護20.4計算檔案...
5 材料模型與性質5.1 本構模型概述5.2 錢彈性模型5.3 各向異性彈性模型5.4 非線彈性雙曲線模型5.5 彈塑性模型5.6 劍橋模型5.7 修正劍橋模型...
7.5.4修正劍橋模型……(267)7.5.5劍橋模型的局限性(270)思考題………(270)習題………(271)第8章土壓力計算(274)8.1概述……(274)8.2靜止...
