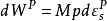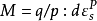劍橋模型是指由英國劍橋大學Roscoe等於1963年提出的，這個模型基於正常固結土和超固結土試樣的排水和不排水三軸實驗基礎上，提出了土體臨界狀態的概念，並在實驗基礎上，再引入加工硬化原理和能量方程，提出劍橋模型。這個模型從試驗和理論上較好的闡明了土體彈塑性變形特徵，尤其考慮了土的塑性體積變形，因而一般認為，劍橋模型的問世，標誌著土本構理論發展的新階段的開始。
基本介紹
- 中文名：劍橋模型
- 外文名：Cambridge model
- 學科：土木工程
- 提出時間：1963年
- 提出人：劍橋大學Roscoe
- 局限性：沒有考慮土的結構性
劍橋模型內容,劍橋模型特點,劍橋模型發展,劍橋模型的局限性,結論,
劍橋模型內容
1958 - 1963 年間, 英國劍橋大學的Roscoe等根據正常固結粘土和弱超固結粘土的三軸試驗, 提出的劍橋粘土的本構模型,標誌著人們在土體力學特性認識上的第一次飛躍。他們將“帽子”屈服準則、正交流動準則和加工硬化規律系統地套用於Cam 模型之中,並提出了臨界狀態線、狀態邊界面、彈性牆等一系列物理概念,構成了第一個比較完整的土塑性模型。Roscoc 和Burland又進一步修正了劍橋模型,認為劍橋模型的屈服面軌跡應為橢圓,給出了現在眾所周知的修正劍橋模型。可以這樣說,劍橋模型開創了土力學的臨界狀態理論。
試驗證明,對於正常固結粘土和弱固結的飽和重塑粘土,孔隙比e 與外力p , q 之間存在有唯一的關係,且不隨應力路徑而發生變化。該模型試圖描述室內試驗所觀察到的現象,即從某一初始狀態開始載入直到最終維持塑性常體積變形的臨界狀態,其基本組成如下:
(1)在( e , p) 平面中,存在一條曲線,在正常固結粘性土中的所有應力遵循此路徑,這被稱為正常固結線(NCL) 。這條線提供了體積硬化規則,可以被廣義化為一般應力條件。
(2) 在( e , p , q) 空間中存在一條線,所有的殘餘狀態都遵循此路徑,而與實驗類別和初始條件無關。這條線與( e , p) 平面中的正常固結線平行,在此線上,剪下變形發生而沒有體積變形發生。
(3) 從固結排水和不排水實驗中所得到的應力路徑位於唯一的狀態面,通稱為Roscoe 面。事實上,在不排水路徑中,土隨著塑性體積應變的發展而硬化。其中,體積應變的彈性和塑性應變增量之和保持常數。Roscoe 面價值在於給出了屈服面類型的一個選擇依據。
模型基於對臨界狀態線、相關聯塑性理論中屈服面與固結定律的假定。該模型假定: ①屈服只與應力球量p 和應力偏量q 兩個應力分量有關,與第三應力不變數無關; ②採用塑性體應變硬化規律,以ev 為硬化參數; ③假定塑性變形符合相關聯的流動法則,即g (s) = f (s) ④假定變形消耗的功,即塑性功為
劍橋模型特點
劍橋模型是當前在土力學領域內套用最廣的模型之一,其主要特點有:基本概念明確;較好地適宜於正常固結粘土和弱超固結粘土;僅有3 個參數,都可以通過常規三軸試驗求出,在岩土工程實際工作中便於推廣;考慮了岩土材料靜水壓力屈服特性、剪縮性和壓硬性。
劍橋模型發展
1、基於經典塑性理論框架的修正
帽蓋模型是Dimaggi 和Sandier ( 1976)在劍橋模型的基礎上提出的。該模型不僅能描述塑性屈服前的非線性、剪脹性等特性,還能描述屈服後的各種破壞性狀與塑性硬化性狀。國內, 魏汝龍(1981)根據不排水三軸壓縮試驗資料得到的正常固結粘土模型,比修正劍橋模型具有更大的適應性,修正劍橋模型僅是它的特例。楊林德、張向霞(2005)針對CamOclay 模型計算中存在沒有充分考慮剪下變形的缺點,首先採用理論分析的手段,指出產生此現象的原因, 同時提出由剪應力和體應力引起的應變分量分別採用不同的分配比例係數的思想。在此基礎上對CamOclay 模型進行了改進。
2、非關聯流動
Banerjee 和Stipho ( 1978 )基於劍橋模型框架,採用塑性增量理論,分析各向同性正常固結及微超固結粘土的不排水應力O應變反映,建立了關聯和非關聯流動的彈塑性本構模型。Newson (1998)提出一個軟粘土非關聯流動的臨界狀態本構模型,其屈服面與修正劍橋模型相同,塑性勢函式為一經驗函式,屈服面與塑性勢面在偏平面上從低應力時的圓形到破壞時的松崗元屈服面。
3、次塑性理論與臨界狀態土力學
Masin將次塑性理論與臨界狀態土力學相結合,建立了一個既適用於正常固結也適用於超固結粘土的本構模型。Masin還利用次塑性模型預測修正劍橋模型的狀態邊界面的存在。
4、有限應變的劍橋模型
Yatomi 等提出了考慮有限應變的劍橋模型,模型中加入了非共軸因素,可模擬土的局部剪下帶。Callari 和Auricchio , Borja 和Ronaldo 等也分別建立了有限應變劍橋本構模型,Ortiz 和Pandolfi 基於劍橋模型框架,建立非粘性土本構模型,具有指數型壓縮曲線,屈服面及塑性勢為橢圓,採用體積應變硬化,模型預測從小應變擴展到有限應變。
5、時間相關的劍橋模型
Hsieh 等利用劍橋塑性理論將粘性土的應力O應變關係加入與時間相關的因素,把總變形分為瞬時應變和粘性應變部分。瞬時應變利用2個屈服面來計算,一個屈服面為修正劍橋模型的橢圓形,另一個用Von Mises 的圓柱形屈服面來描述,Arai 等,Namikawa 分別結合劍橋模型建立了依賴時間的正常固結粘土的塑性模型,Arai 的模型還考慮了粘土各向異性K0 固結對應力O應變關係的影響。Liao 等基於修正劍橋模型與Perzyna 粘塑性方程,運用相關聯與不相關聯的塑性流動法則,建立了一個反映時間效應和剪脹行為的本構模型。Yin 和Graham基於修正的劍橋模型建立了一個彈粘塑本構模型,這個模型能模擬加速蠕變、卸荷再載入、松馳等軟粘土變形行為。
6、考慮各向異性及結構性日本學者太田和關口提出了反映各向異性和應力軸旋轉的關口O太田模型,並被廣泛套用於日本的工程實踐中。其精華在於引進新的應力比,使劍橋模型成為其特例,能考慮K0 固結引起的應力各向異性,和主應力軸旋轉產生的塑性變形。但不能考慮中主應力的影響,即不能考慮真正三維的應力狀態。
劍橋模型沿球應力軸( p 軸) 為等向塑性體變硬化,在日本廣泛採用的關口O太田模型沿初始固結線( K 0 線) 為不等向塑性體變硬化。三軸試驗數據表明:自K0 狀態向伸長方向剪下時,前者方法計算的體積應變偏小,而後者方法計算的體積應變偏大。孫德安、姚仰平、殷宗澤提出一種介於上述兩者之間、考慮初始應力各向異性(如K 0 固結) 的不等向塑性體變硬化彈塑性模型。模型的剪下屈服準則使用SMP 準則,該模型能在三維應力下較好地反映土的強度和變形特性,模型的土性參數與劍橋模型一樣。
Voyiadjis 等基於Dafalias 的各向異性修正劍橋模型建立了一個新的考慮體土的各向異性和結構性的本構方程,利用了一個稱為塑性旋轉張量的內變數,這個塑性旋轉張量是引起各向異性的背應力的函式, 模型增加了2 個背應力參數。Wheeler 等利用多階段三軸排水試驗的數據,改進修正劍橋模型,建立了飽和軟粘土各向異性本構模型。Liu 和Carter 將土的結構性加入修正劍橋模型,3 個新的參數用來描述土的結構性,如果所模擬的土無結構性,該模型等同於修正劍橋模型。John 和Carter 等提出一個土的結構性劍橋模型,這個模型基於臨界狀態框架,能考慮天然粘土的當前應力狀態、應力歷史、當前孔隙比和當前土的結構,採用塑性體應變硬化。
針對修正劍橋模型僅適用於正常固結及弱固結粘土,而不適用於嚴重超固結土的情況, Amerasin和Kraft ,Banerjee 等建立了嚴重超固結土的劍橋模型。Mita 和Dasari 等基於嚴重超固結土的三軸壓縮O伸長試驗及平面應變試驗,建立了一個伏斯列夫O修正劍橋( HvorsleOMCC) 模型, 模型具有伏斯列夫面, 採用MohrOCoulomb 屈服準則,並被擴展到一般三維應力空間。
劉元雪,施建勇從岩土類材料極限應力狀態線所致的各向異性出發,提出了應力空間變換思想。以修正劍橋模型屈服面的中心為映射中心,給出了重塑土的應力空間變換、應力增量變換的公式, 並考慮了應力洛德角的影響。在變換應力空間中對修正劍橋模型進行了重新表述與改進,該模型可以較好地反映各向異性的影響,反映三軸伸長等應力路徑的應力應變特性,也反映某些路徑所致的軟化現象。
7、循環荷載下的臨界狀態模型
Carter 和Booker 等, Hirai 和Hi2royoshi分別建立了循環荷載下的臨界狀態模型,後者採用非關聯流動法則,屈服面及塑性勢均為劍橋模型形式。Nova 和Roberto基於劍橋模型,建立了模擬循環荷載下粘土或砂土變形特性的彈塑性本構模型,可模擬土的遲滯、模量衰化及液化等行為。Rouainia 和Wood提出了一個天然粘土的率相關本構模型,該模型是劍橋模型的擴展,建立在邊界麵塑性的運動硬化框架內,可考慮塑性應變引起的結構損傷。Borja 和Ronaldo等將經典修正劍橋模型與具有橢圓載入函式的各向異性邊界麵塑性模型結合,該模型還耦合非線性超彈性模型。
8、擴展到一般三維應力空間
Nakai 等基於SMP 屈服準則,建立了一個在三維應力空間模擬粘土各種不同應力路徑下行為的本構模型,模型不僅考慮了中主應力的影響,也反映了應力路徑對土體應力與應變關係的影響。模型參數確定方法與劍橋模型相同。Matsuoka 等採用SMP (空間滑動面) 準則對劍橋模型進行了擴展,將劍橋模型從三軸試驗的軸對稱應力狀態擴展至一般應力狀態,其修正的方法是引入變換應力,重新定義變換後的廣義正應力和剪應力,然後代入劍橋粘土模型中,實現從Mises 破壞準則向SMP 破壞準則的擴展。姚仰平等將Lade 屈服準則引入最初的劍橋模型,以實現模型的三維化,採用變換應力將Lade 屈服準則變為擴展的Mises 屈服函式類型。孫德安,姚仰平又提出了一個適用於粒狀材料的簡單而實用的彈塑性模型。該模型通過對修正劍橋模型進行改進,能夠反映三維應力狀態下的剪脹剪縮性和變形、強度的平均應力依存性。姚仰平等還把Mohr O Coulomb 準則與劍橋模型相結合,提出了一個變換應力張量,在主應力空間上,將Mohr O Coulomb 準則變為圓錐形,能描述一般應力空間土的變形特性。
9、擴展到砂土、非飽和土
Borja 和Ronaldo將經典修正劍橋模型從飽和粘土擴展到非飽和土。Robinet 等建立了適用於膨脹土,具有兩個屈服面的修正劍橋模型形式的本構方程。砂土的變形行為不僅依賴於其相對密度也依賴於所處的固結壓力。同一固結壓力下,密砂剪脹,松砂剪縮;同一密度的砂,在低固結壓力下可能剪脹,而在高固結壓力下則可能剪縮。在臨界狀態理論的框架內,為了統一反映密度和壓力對砂土變形特性的耦合影響, Been 和Jefferies建議了一個狀態參數,把圍壓和密度的耦合作用加入到本構方程中,其中, Yu提出一個對粘土和砂土都適用的統一臨界狀態模型,採用應力比與狀態參數的關係來描述土的狀態邊界面,重新定義了屈服函式及塑性勢函式,模型適用範圍廣,相對簡單,與劍橋模型相比,僅增加2 個參數。Gajo 和Wood基於劍橋臨界狀態概念,小應變彈性區假定,狀態參數概念,劍橋模型的流動法則,邊界面概念和運動硬化塑性,建立了一個反映較大範圍孔隙比和應力水平的粒狀材料本構模型。
劍橋模型的局限性
縱觀劍橋模型40 多年的發展,總結其局限性主要有:
(1) 受制於經典塑性理論,採用Drucker 公設和相關聯的流動法則,在很多情況下與岩土工程實際狀態不符;破壞面有尖角,該點的塑性應變方向不易確定。
(2) 因為屈服面只是塑性體積應變的等值面,只採用塑性體積應變作硬化參量,因而沒有充分考慮剪下變形; 只能反映土體剪縮,不能反映土體剪脹;因此不適用於強超固結粘土和密實砂,在工程套用範圍上受限制,並且對於水平位移無法得出符合實際的結果。
(3) 沒有考慮土的結構性這一根本內在因素的影響。以後提出的彈塑性模型中許多都是從劍橋模型派生出來的,它們與劍橋模型的缺陷一樣,都是從重塑土的概念出發建立的。沒有考慮天然粘土的結構性,因而得出的結果都不盡滿意;也不能合適地模擬結構與應力誘導的各向異性。
(4) 採用各向同性硬化,不能用於描述循環剪下荷載條件,在此條件下觀察到應力O應變具有高度的非線性,迥滯圈斜率依賴於加卸載條件。
(5) 未能反映剪脹對於有效應力比的依賴性,這一現象在絕大部分無粘性土中均可見到。
(6) 未能考慮粘性土的由粘性引起的與時間相關的應力應變關係。 (7) 模型適用於軸對稱應力狀態,沒有計及中主應力對強度和變形的影響,不適用於一般的三維 應力空間。
(8) 其假定的彈性牆內載入仍會產生塑性變形。
結論
目前,儘管針對岩土材料的各種建模思想不斷湧現,出現了各種不同形式的土體本構模型,但是彈塑性模型中,劍橋模型與修正的劍橋模型是得到公認的為數不多的模型之一。而由此發展起來的臨界狀態理論,更具有明確的幾何與物理意義,是其它許多模型無法比擬的。臨界狀態是岩土的一種極限狀態,它可作為岩土的一種變形關係,補充到極限平衡的分析中,對岩土臨界狀態下的變形或流動規律的研究與探討,尤其對砂土,有重要的理論意義和實際工程意義。另外,在劍橋模型基礎上針對其局限性進行改進和修正,仍是岩土材料建模的重要方向。
