基本介紹
- 中文名:依數性
- 外文名:colligative properties
- 別稱:依數性質
- 提出者:拉烏爾,范特霍夫,亨利
- 提出時間:1887
- 套用學科:化學
- 適用領域範圍:溶液的性質
- 適用領域範圍:測定含量
發現簡史,相關概念,蒸氣壓下降,實驗驗證,現象解釋,數學推導,套用領域,沸點升高,現象內容,現象解釋,數學推導,套用領域,凝固點下降,現象內容,注意事項,現象解釋,數學推導,套用領域,滲透壓,現象內容,現象解釋,滲透壓定律,數學推導,套用領域,揮發性溶質溶液的依數性,溶質揮發性大於溶劑揮發性,溶質揮發性小於溶劑揮發性,正偏差,負偏差,電解質溶液的依數性,電離學說,活度與離子強度,強電解質理論,套用領域,濃溶液的依數性,溶劑化,粒子半徑,分子極性與范德華力,
發現簡史
拉烏爾(又譯婁爾特Raouh)和普費弗(Pfeffer)的基本研究工作奠定了近代溶液理論的基礎。溶液的依數性的發現是伴隨著溶液的滲透壓、凝固點下降、沸點升高和蒸汽壓下降等現象的發現和理論的提出而逐漸發展的。
滲透壓的發現
18 世紀中葉,安托萬·諾萊(Abbé Nollet) 發現:水能自然地透過豬膀朧擴散到酒精溶液內。他首次揭示了膜分離現象,但限於當時的認識能力,尚不知此為滲透壓問題。首先探明滲透壓力問題的是特勞伯(M.Traube),他在1867年實驗人造植物細胞時,發現了一種由亞鐵氰化銅(cupric ferrocyanide)製成的半透膜。但由於這種半透膜不夠堅固的原因,欲測定滲透壓的絕對數值頗不容易。1877年萊比錫大學植物教授威廉·普費弗將亞鐵氰化銅沉積在素瓦罐壁有孔盆上,製得適用而強固的半透膜,它可以只讓水通過而不讓溶解的糖透過去,於是普費弗用這種半透膜測量了多種溶液的滲透壓,由此發現滲透壓與溶液濃度成正比。但是除植物學家外,這個結論並未眾人所熟知。1884年阿姆斯特丹植物學家德·福利斯(de Vries)特別研究了等滲溶液,並將其研究告訴范特霍夫後,范特霍夫立即看出它在物理化學上的偉大意義。范特霍夫結合普費弗的實驗數據和查爾斯等定律並運用熱力學證明了:溶質在溶液中產生的滲透壓等於占有和溶液相同體積的氣體產生的壓力。其滲透壓定律便可以用理想氣體狀態方程推算。但在譬如鹽酸、強鹼和鹽等溶液中好像有的代表二倍分子數,當時,范特霍夫發表其溶液學說時,尚不明白為什麼有此類現象,於是用一個因子“i”放入方程式中,以表示反常大的滲透壓。
凝固點下降的發現
鹽水比淡水的凝固點低些的事實,早在1788年卡文迪許(又譯凱文第旭)的助手布萊格登(Blagden)就首先研究過,他知道同一化合物的溶液的凝固點下降值和濃度有比例關係,但此後100年,此問題尚未有合理的解釋。直至1878年拉烏爾發表了關於溶液凝固點的第一篇著作,1881年烏拉爾教授主要用有機物進行多次實驗,並把結果在1882年列成一張表,表中所示100克水中含有1克的物質的溶液,其凝固點的下降與此物質的相對分子質量的乘積是一個常數。他說:“這似乎證明,在大多數情況下,有機化合物的分子,被溶解作用簡單的分開,成為相同的狀態,對水的物理性質產生同樣的影響。”
他把凝固點下降數值稱為“下降係數”(depression coefficient),把下降係數和分子量的乘積的常數,稱為“分子下降”(molecular depression),經其種種實驗,他發現有機化合物的分子下降乃是分子其中各個原子的“原子下降”的平均數。至於原子下降是原子的本性,可算出C、H、O、N的原子下降是15、15、30、30,一常規有機化合物CpHqOrNs的分子下降,為(15p+15q+30r+30s)/(p+q+r+s),他說只要測出下降係數,便可推算出一個化合物的分子式。舉草酸為例,通過燃燒和分析等,草酸的實驗式CHO2,其可能分子式C2H2O4、C3H3O6等,但無論用那個分子式,算出的分子下降都是22.5。烏拉爾測得草酸下降係數為0.255。故其大概分子量22.5/0.255=88.3,故知C2H2O4(分子量為90)為草酸的正當分子式,這種發現立即引起有機化學家的注意,因為以前無可靠方法測定不揮發物質的分子量,可以在溶液中測定了。但是,拉烏爾尋求某些化合物的分子下降值時,有時竟然有兩個,且一個差不多是另一個的兩倍,發現醋酸的值有18和39,甲酸有14和28,硝基苯有36和72,二溴化乙烯有58和118等等,按照烏拉爾實驗,許多鹽類、強酸、和強鹽基的為何都有異常大的凝固點下降和沸點上升,是後來從其他方面才得到的解釋。
沸點升高的發現
沸點升高的現象也久為人知,1822年法拉第(Faraday)、1824年格里菲斯(Griffiths)和1835年勒格朗(Legrand)也都考察過,尚不得要領。及拉烏爾做過凝固點下降和其他實驗後,才證明沸點上升的規律和凝固點下降相似。
蒸氣壓下降的發現
早在1822年就已經知道溶液的蒸氣壓,比純溶劑的低,但到1855年Wüllner才用實驗發現,如果溶質是不揮發的,則溶液的蒸氣壓下降與溶解物質的數量有比例關係。1886-1887年拉烏爾證明:“1克分子固定的、非言物質,溶解在100克分子任何揮發性液體中,液體蒸氣壓的降低是其蒸氣壓數字的接近不變的分數,這分數大約是0.0105。”這又是一個用溶液來求相對分子質量的方法。1887年拉烏爾用萜烯、硝基苯、苯胺、甲酯和苯甲酸乙酯5種化合物,取每種各異數量,放於水、二硫化碳、四氯化碳、丙酮、戊烯、苯等11種溶劑中。其結果都是:只要在100溶劑分子中的溶質分子數不大於15,溶液蒸氣壓下降數值與溶質的分子數目有比例關係。又以分子重量為比例,將各物質溶於等容的同一溶劑中,蒸氣壓下降的數值都相等。又發現一個規則:蒸氣壓的下降值與原來蒸氣壓的比值即下降率等於溶質分子數與溶液分子總數的比值。由此與1887年發現拉烏爾定律,並於理論方面找出凝固點下降和沸點上升與蒸氣壓下降的關係,此時范特霍夫的溶液學說也已經成立,又找出它們三者和滲透壓的關係,於是在溶液中測定有機分子量有了確切的理論基礎。
電解質理論的發現
對於拉烏爾曾經注意到的異常的分子下降和范特霍夫對鹽類溶液的異常偏大的滲透壓,首次完全給出解釋的是阿侖尼烏斯(Arrhenius)的電離理論。但這個學說套用在弱電解質上最為相宜,不能套用於強電解質,雖然有試驗的公式來表示強電解質的行為,但都無理論上的依據。直到1923德國化學家德拜(Debye)和休克爾(Hückel)提出的離子互吸理論才將其合理化。但較濃的溶液中離子相隔較近,所引起的完全反乎電離的行為不斷增大,至今電解質溶液理論仍然在不斷完善中。
相關概念
稀溶液與純溶劑相比某些物理性質會有所變化如蒸氣壓下降、凝固點降低、沸點升高和滲透壓的產生。這是多組分系統中化學勢隨組分數而表現出來的自身變化規律,溶液的依數性只有在溶液的濃度很稀的時候才有規律,而且溶液越稀,其依數性的規律性越強。
除此之外,依數性還受到溶質的電解性和揮發性的影響。
溶液按電解質在溶液中的電離程度可將溶液分為非電解質溶液和電解質溶液,其中電解質溶液又有強電解質溶液和弱電解質溶液之分;在一定溫度下,不同物質有不同的蒸氣壓。通常把常溫下蒸汽壓較低的物質稱為難揮發物質,如甘油、葡萄糖、食鹽等;蒸氣壓較高的物質稱為易揮發物質,如苯、乙醇、碘等。所以蒸氣壓越大,越易揮發,沸點越低。

由於至今電解質理論和濃溶液理論論仍在不斷完善中,而揮發性溶質的依數性偏差波動很大,故本詞條著重討論溶劑為難揮發非電解質的稀溶液的依數性。
蒸氣壓下降
實驗驗證
實驗一,見右圖:在一封閉容器,放一杯純水和濃溶液(濃糖水)。經過一段時間後,發現糖水的液面面上升了,純水的液面下降。水蒸氣會不斷的凝聚於糖水中,直到水杯中的水全部轉移到糖水杯中為止。這個實驗被稱為溶劑轉移實驗。

這隻有假設糖水的蒸氣壓比水的蒸氣壓低才顯得合理,因為在這個密閉的容器里,有三個水的蒸氣壓:純水的蒸氣壓代表純水的蒸發速度,密閉容器的空氣中的水蒸氣壓代表水的凝聚速度,以及糖水的蒸氣壓代表糖水的蒸發速度。顯然純水的蒸發速度大於水的凝聚速度,導致純水的液面下降;糖水的蒸發速度小於水的凝聚速度,導致液面的上升;這說明了純水的蒸氣壓大於密閉容器中的水蒸氣壓大於的糖水的蒸氣壓。而且這一實驗通過水的轉移時間,可以證明溶液濃度越大,溶液的蒸氣壓下降的越顯著。
實驗二,初始狀態見左下圖的裝置中,左管是純水,右管為葡糖糖溶液,兩管由U形壓強計相連,U型管中的水銀高度相同。關閉閥門,置水浴恆溫。然後打開閥門,一定時間後,見右下圖,可觀察到壓強計的水銀面右柱高於左柱,表明葡萄糖溶液的蒸氣壓小於水的蒸氣壓。而且這一實驗通過水銀液差,可以證明溶液濃度越大,溶液的蒸氣壓下降的越顯著。


現象解釋
當純溶劑溶解一定量難揮發溶質(如蔗糖溶於純水時,萘溶於苯中)時,在同一溫度下,溶液的蒸汽壓總是低於純溶劑的蒸汽壓。這種現象稱為蒸汽壓下降,即

式中 ---溶液的蒸氣壓下降值;
---溶液的蒸氣壓下降值;



稀溶液蒸氣壓下降的原因可以從以下兩個方面來解釋,如下圖所示:一方面,溶質分子占據著一部分溶劑分子的表面,在單位時間內逸出頁面的溶劑分子數目相對減少;另一方面,在溶劑中加入了難揮發的非電解質後,每個溶質分子與若干個溶劑分子相結合,形成了溶劑化分子,溶劑化分子一方面束縛了一些能量較高的溶劑分子。因此,達到平衡時,溶液的蒸氣壓必定低於純溶液的蒸氣壓,且濃度越大,蒸氣壓下降越多。這也是解釋沸點升高和凝固點下降更為根本的原因。

數學推導
對於兩組分溶液,由道爾頓分壓定律,注意在體系的氣相中純溶劑蒸氣壓代表了總的壓強,而溶液的蒸氣壓由於非電解質分子的阻隔和溶劑化作用,相當於總氣壓的分壓:

拉烏爾定律
1887年,法國物理學家拉烏爾(F.M.Raoult)研究了溶質對純溶劑蒸氣壓的影響,根據大量實驗結果提出下列三個觀點,這些規律稱為拉烏爾定律,拉烏爾定律證明了蒸氣壓下降與溶液組成的不同量度之間的關係,在此一一證明論述。
在一定溫度下,難揮發非電解質稀溶液的蒸氣壓,等於純溶劑的蒸氣壓乘以溶劑A在溶液中的摩爾分數(一說物質的量分數)。其數學表達式: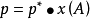
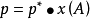
用x(B)表示難揮發非電解質的物質的量分數,

所以,

用 表示溶液的蒸氣壓下降值,
表示溶液的蒸氣壓下降值,


上式表明,拉烏爾定律又可以表示為:在一定溫度下,難揮發非電解質稀溶液的蒸氣壓下降 與溶質B摩爾分數成正比。
與溶質B摩爾分數成正比。

其數學表達式為:

對於兩組分溶液:

當溶液很稀時,溶質B的物質的量小到可以忽略不計:

即

當溫度一定時,p*和M(A)都是常數,其乘積用K表示,則:

因此,拉烏爾定律又可以表述為,在一定溫度下,難揮發非電解質稀溶液的蒸氣壓下降,近似地與溶質B的質量摩爾濃度成正比,而與溶質的本性無關。
套用領域
溶液凝固點下降在冶金工業中具有指導意義。一般金屬的Kf都較大,例如Pb的Kf≈130 K kg/mol,說明熔融的Pb中加入少量其它金屬,Pb的凝固點會大大下降,利用這種原理可以製備許多低熔點合金。金屬熱處理要求較高的溫度,但又要避免金屬工件受空氣的氧化或脫碳,往往採用鹽熔劑來加熱金屬工件。例如在BaCl2(熔點1236 K)中加入5%的NaCl(熔點1074 K)作鹽熔劑,其熔鹽的凝固點下降為1123 K;若在BaCl2中加入22.5%的NaCl,熔鹽的凝固點可降至903 K。
沸點升高
現象內容
當液體的蒸氣壓等於外壓時,液體的汽化將在其表面和內部同時發生,這種汽化過程稱為液體的沸騰,此時再給體系加熱,只會使更多的液體汽化,而體系的溫度不會上升。沸點Tb(boiling point)是當純液體或溶液的蒸氣壓與外界大氣壓相等時,溶液沸騰的溫度。值得注意的是,沸點與外壓有關,外壓越大,沸點越高。
沸點升高的現象特徵可以從右圖的純水與水溶液的相圖觀察得出。圖中,縱坐標為蒸氣壓,橫坐標為體系溫度。ab曲線為純水的蒸氣壓隨溫度變化曲線,a‘b’曲線為水溶液的蒸氣壓隨溫度變化的曲線。從a‘b’曲線在ab曲線下方,可以看出水溶液的蒸氣壓在任何溫度都小於純水的蒸氣壓。
如果未指明外界壓力,默認外界大氣壓為101.325 kPa。在373.15K時,水的蒸氣壓等於外界大氣壓,所以水的沸點是373.15K(100℃)。在右圖中,當縱坐標等於外界大氣壓(101.3kPa)時,水的正常沸點Tb*小於水溶液的沸點Tb。這種溶液的沸點高於溶劑沸點的現象為溶液的沸點升高。
溶液的沸點升高的數值ΔTb等於溶液的沸點Tb與純溶劑的沸點Tb*之差:

現象解釋
之所以會出現溶液的沸點高於純溶劑沸點的現象,是因為在溶劑加入少量難揮發的非電解質後,所形成的溶液由於蒸氣壓下降,其蒸氣壓低於外界大氣壓,故溶液達到純溶劑的沸點時,仍不能沸騰。於是要使溶液沸騰,必須繼續升高溫度,使得溶液的蒸氣壓達到外界壓力,其溫度已經超過純溶劑的沸點,所以這類溶液的沸點總是比純溶劑的沸點高。
由於溶液的沸點升高的根本原因是溶液的蒸氣壓下降,所以,溶液濃度越大,則蒸氣壓下降的越多,於是沸點升高得越多。而且溶液沸點升高是由於溶液蒸氣壓下降引起的,對於難揮發非電解質的稀溶液,既然蒸氣壓下降和溶液的質量摩爾濃度b(B)成正比,這類溶液的沸點升高也應和質量摩爾濃度有聯繫。類似地,拉烏爾(Raoult)根據依數性指出:難揮發非電解質稀溶液的沸點升高也近似地與溶質B的質量摩爾濃度成正比,即
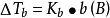
式中:Kb稱為沸點升高常數(boiling point constant),單位為K·kg·mol-1或℃·kg·mol-1,這個數值只取決於溶劑,而與溶質無關。沸點升高常數的計算公式:

式中: 是純溶劑的摩爾汽化熱,R為摩爾氣體常量,Tb*為純溶劑的沸點,MA為溶劑A的摩爾質量。
是純溶劑的摩爾汽化熱,R為摩爾氣體常量,Tb*為純溶劑的沸點,MA為溶劑A的摩爾質量。

溶劑 | 沸點Tb/K (t/℃) | Kb/K·kg·mol-1 |
水 | 373.15(100) | 0.512 |
苯 | 353.25(80.1) | 2.53 |
乙醇 | 351.65(78.5) | 1.22 |
乙酸 | 391.05(117.9) | 3.07 |
丙酮 | 329.35(56.2) | 1.71 |
四氯化碳 | 349.70(76.6) | 5.03 |
萘 | 491.15(218.0) | 5.80 |
酚 | 454.35(181.20) | 3.60 |
乙醚 | 307.85(34.70) | 2.02 |
環己烷 | 354.15(81) | 2.79 |
樟腦 | 481.15(208) | 5.95 |
參考資料來源
數學推導
揮發性溶劑A在正常沸點Tb*時存在下述液-氣平衡:A(1,Tb*,pΘ)⇌A(g,Tb*,pΘ)
根據相平衡關係,其平衡條件為μAΘ(1,Tb*)=μAΘ(g,Tb*) (1)
當向溶劑A加入非揮發性溶質B後,溶液的正常沸點為Tb。此時的液-氣平衡條件為
μAΘ(1,Tb*)+RTblnxA=μAΘ(g,Tb) (2)
因為△vapGmΘ,A(Tb)=μAΘ(1,Tb*)-μAΘ(g,Tb*)
(1)、(2)兩式可以整理為:△vapGmΘ,A(Tb)/Tb*=0,△vapGmΘ,A(Tb)/Tb=RTblnxA
相減得△vapGmΘA(Tb)/Tb*-△GmΘ,A(Tb)/Tb=-RTblnxA
當溫度溫度變化較小,吉布斯-亥姆霍茲公式的積分形式:
△G(T2)/T2-△G(T1)/T1=-△H(T2-T1)/T1T2
將此公式套用到上式,整理可得:
-lnxA=△vapHmΘ,A(Tb-Tb*)/RTbTb*≈△vapHmΘ,A· ΔTb/R(Tb*)2,其中TbTb*近似為(Tb*)2。
對於二元稀溶液,xA→1,xB→0,-lnxA=-ln(1-xB)≈xB≈nB/nA
n為溶液中A、B的物質的量,於是可寫成:ΔTb=nBR(Tf*)2/nA△vapHmΘ,A
若用b(B)表示質量摩爾濃度,M表示摩爾質量,m表示質量,又可寫成:
ΔTb=MAmBR(Tb*)2/MBmA△vapHmΘ,A=b(B)·MAR(Tb*)2/△vapHmΘ,A=Kb·b(B)
以上,是此公式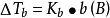 的證明過程,即拉烏爾根據依數性指出:難揮發非電解質稀溶液的沸點升高近似地與溶質B的質量摩爾濃度成正比的數學證明過程。
的證明過程,即拉烏爾根據依數性指出:難揮發非電解質稀溶液的沸點升高近似地與溶質B的質量摩爾濃度成正比的數學證明過程。
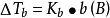
套用領域
鋼鐵工件進行氧化熱處理就是套用沸點升高原理。用每升含550~650 g NaOH和100~150 g NaNO2的處理液,其沸點高達410~420 K。
在鋼鐵冶煉工業中,通過觀測鋼水的沸點來確定其他組分的含量在鋼鐵工業生產中,技術員為了配比一定比率的固溶體需要不斷的取樣測定,不僅重複勞動、工作量大,而且高溫作業採樣會有很大的潛在危險,於是技術員通過觀測安裝在熔爐中溫度測量儀測定每一個狀態時的沸點,就可以確定即時合金中的其他金屬的含量,對合金生產起到關鍵的調控作用.這就依據依數性的沸點上升原理,在純鐵水中加入另一種金屬後沸點會升高,不同的組分含量就對應相應的沸點,通過沸點的變化值就可計算出在某一沸點時另一種金屬的含量,對鋼鐵合金的調節既方便又簡捷。
計算公式為: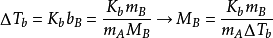
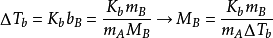
凝固點下降
凝固點是物質在一定的外壓下,其液相蒸氣壓和固相蒸氣壓相等,此時液體的凝固和固體的熔化處於平衡狀態,從溶液中開始析出溶劑晶體時的溫度的溫度。溶液的凝固點實際上就是溶液中的蒸氣壓與純固體溶劑的蒸氣壓與純固體溶劑的蒸氣壓相等時的溫度。
現象內容
凝固點下降的現象特徵可以從純水與溶液的步冷曲線觀察出。物質的溫度隨時間而變化的曲線,叫做步冷曲線。在步冷曲線中,縱坐標為溫度,橫坐標為時間,如右圖所示。

曲線(1)是純水的步冷曲線,AB段是H2O的液相,溫度不斷下降。B點開始結冰,BC段表示溫度不變;在C點處純水全部結冰,CD段表示凍的溫度不斷下降。
曲線(2)是稀溶液的步冷曲線,.A’B’段是液相,溫度不斷下降;B’點低於273K,是溶液的冰點,B’C’段溫度不恆定,有冰析出,隨著溶劑不斷結晶析出,溶液濃度將不斷增大,凝固點也將不斷下降,所以凝固點不恆定;C’點時,冰和溶質一同析出,且二者具有固定的比例。即和此時溶液的比例相同。C’點的溫度稱為低共熔點,從C’點析出的冰鹽混合物,叫低共熔混合物,即兩種或兩種以上物質形成的熔點最低的混合物。
曲線(3)是同溶質的濃溶液的步冷曲線。觀察三條曲線,不難看出B”的溫度比B’溫度低,B‘的溫度比B溫度低,即溶液的冰點下降,且隨著溶液的濃度增加,冰點更低。這種溶液的凝固點低於純溶劑的凝固點的現象稱為溶液的凝固點下降。
即有溶液的凝固點下降的數值ΔTf等於純溶劑的沸點Tf*與溶液的沸點Tf與之差,即

注意事項
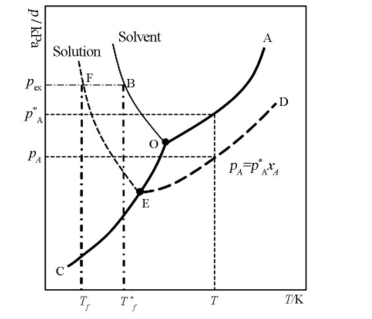
但是有學者指出,上面的凝固點降低的圖解顯然錯了。標準凝固點或標準熔點是指標準態壓力下液態與固態處於平衡的溫度 。純水的凝固點和水溶液的凝固點應當是左圖上的B點和F點。凝固點下降值則為兩點之差 ,但絕不是上圖的稀溶液的氣 - 液曲線向左下方延至其液氣 - 固曲線的交叉點 ,那個點是水的三相點而非凝固點。目前只有少數教材所用的圖解是對的,因為多數教材將沸點升高和凝固點下降放到一個圖中討論了。
誤差在於水的三相(O)點是指純水在固液氣三相同時存在達到平衡時其所對應的狀態,溫度為273.16K,壓強為611.775Pa。水的凝固點(B)點是指飽和空氣的水溶液在1atm下凝固時對應的狀態,溫度為273.15K,壓強為101.325Pa。雖然二者溫度相差0.01K,而壓強相差極大。圖中,OA、OB和OC分別表示純溶劑水的氣-液,液-固和固-氣兩相平衡線,依據純組分兩相平衡熱力學,它們都滿足克拉貝龍方程,其中OA和OB線還滿足克勞修斯-克拉貝龍方程;由於水凝固時體積增大,所以OB線斜率為負值,O點為三相點;在OB線左邊的虛線EF為稀溶液的凝固點隨外壓的變化。
現象解釋

溶液的凝固點下降原因的與沸點升高一樣,本質上都是由於溶液的蒸氣壓下降所引起的。這是因為溶質分子和溶劑化分子對凍的蒸發阻隔作用不大,即對凍的蒸氣壓影響不大,所以溶液的蒸氣壓下降的多,其蒸氣壓必然低於凍的蒸氣壓,即溶液的凝固速度小於凍的蒸發速度,這樣原本的凝固點的溫度不能使得固液平衡了。要使溶液凝固,就必須讓溶液的蒸氣壓和凍的蒸氣壓相等,即此時的溫度應該還要比原先凝固點還要低。
若進一步降低溶液的溫度,溶液和凍的蒸氣壓會同時下降,且由於凍的蒸氣壓的下降率比水溶液的蒸氣壓大,溶液的蒸氣壓和凍的蒸氣壓會在凝固點以下的某一溫度下達到平衡狀態。如溶液凝固點下降圖所示,此時溶液的蒸發速度與凍的蒸發速度與溶液的凝聚速度相等後,對應溫度即溶液的現在的凝固點,這就是凝固點下降的原理。
既然溶液的凝固點下降也是由於溶液蒸氣壓下降引起的對於難揮發非電解質的稀溶液,那么類似的,這類溶液的凝固點下降也應和質量摩爾濃度b(B)有聯繫。拉烏爾根據依數性指出:對於難揮發非電解質的稀溶液,凝固點下降ΔTf都和溶液質量摩爾濃度成正比,即

式中:Kf稱為凝固點下降常數(freezing point constant),單位為K·kg·mol-1或℃·kg·mol-1,這個數值只取決於溶劑,而與溶質無關。下面是凝固點下降常數Kf的計算公式:

式中: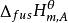 是純溶劑的摩爾熔融焓,R為摩爾氣體常量,Tb*為純溶劑的沸點,MA為溶劑A的摩爾質量。
是純溶劑的摩爾熔融焓,R為摩爾氣體常量,Tb*為純溶劑的沸點,MA為溶劑A的摩爾質量。
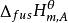
溶劑 | 沸點Tf/K (t/℃) | Kf/K·kg·mol-1 |
水 | 273.15(0) | 1.86 |
苯 | 278.50(5.35) | 5.12 |
硝基苯 | 278.85(5.70) | 6.90 |
乙酸 | 289.75(16.6) | 3.90 |
環己醇 | 279.69(6.54) | 39.30 |
四氯化碳 | 250.20(-22.95) | 29.8 |
萘 | 80.30(353.45) | 5.12 |
酚 | 313.15(40) | 7.27 |
環己烷 | 279.65(6.5) | 20.20 |
樟腦 | 351.15(78) | 40.00 |
參考資料來源
Kf和Kb的數值均不是在b(B)=1mol·kg-1時測定的,因為許多物質當其質量摩爾濃度遠未到1mol·kg-1時,拉烏爾定律已不適用。此外,還有許多物質的溶解度很小,根本不能形成1mol·kg-1溶液,實際Kb和Kf值是從稀溶液的一些實驗結果推算而得出的。
數學推導
純溶劑A在正常凝固點Tf*時存在下述固-液平衡:A(s,Tf*,pΘ)⇌A(1,Tf*,pΘ)
根據相平衡關係,其平衡條件為μAΘ(s,Tf*)=μA(1,Tf*) (1)
當向溶劑A加入溶質B後,溶液的正常凝固點為Tf。設只有A結晶析出,B不結晶析出。則體系固-液平衡為
μAΘ(s,Tf*)=μAΘ(1,Tf) +RTblnxA (2)
因為△fusGmΘ,A(T)=μAΘ(1,T)-μAΘ(g,T)
(1)、(2)兩式可以整理為:△fusGm,A(Tf*)/Tf*=0,△fusGm,A(Tf)/Tf=-RTflnxA
相減得△fusGm,A(Tf)/Tf-△fusGm,A(Tf*)/Tf*=-RTflnxA
當溫度溫度變化較小,吉布斯-亥姆霍茲公式的積分形式:
△G(T2)/T2-△G(T1)/T1=-△H(T2-T1)/T1T2
將此公式套用到上式,整理可得:
-lnxA=△fusHmΘ,A(Tf*-Tf)/RTfTf*≈△fusHmΘ,A· ΔTf/R(Tf*)2 ,其中TfTf*近似為(Tf*)2。
對於二元稀溶液,xA→1,xB→0,則-lnxA=-ln(1-xB)≈xB≈nB/nA
n為溶液中A、B的物質的量,於是可寫成:ΔTf=nBR(Tf*)2/nA△fusHmΘ,A
若用b(B)表示質量摩爾濃度,M表示摩爾質量,m表示質量,又可寫成:
ΔTf=MAmBR(Tf*)2/MBmA△fusHmΘ,A=b(B)·MAR(Tf*)2/△fusHmΘ,A=Kf·b(B)
以上,是此公式 的證明過程,即拉烏爾根據依數性指出:對於難揮發非電解質的稀溶液,凝固點下降ΔTf都和溶液質量摩爾濃度成正比的數學證明過程。
的證明過程,即拉烏爾根據依數性指出:對於難揮發非電解質的稀溶液,凝固點下降ΔTf都和溶液質量摩爾濃度成正比的數學證明過程。

套用領域

比起沸點升高法,實際套用中常使用冰點降低法進行測定,因為溶液的凝固點可以精確測定,原因有三:一是部分高分子生物樣品和有機物在高溫下容易破壞;二是高溫下因為揮發而引起濃度變化時不能重複測定Tb;三是溶劑的凝固點降低常數比沸點升高常數大,測定結果的精確度較高。
有機化學還用測定沸點的升高和凝固點的下降來檢驗化合物的純度,這是因為含雜質的化合物可以看作是一種溶液。
滲透壓
現象內容
產生滲透作用有兩個必要條件:一是有半透膜存在;半透膜兩側存在濃度差。在如右圖所示的容器中,左邊盛純水,右邊盛糖水,連通容器中間安裝一種小(溶劑)分子可通過,大(溶質)分子卻不能通過的具有選擇性的半透膜(semi-permeable membrance),如羊皮紙、火棉膠膜、玻璃紙、動植物細胞膜、毛細血管壁等物質都具有半透膜的性質。

開始時,a容器兩側液面等高。經過一段時間以後,可以觀察到b容器左側純水液面下降,右端糖水液面升高,說明存水中有一部分水分子通過半透膜進入了溶液,這種溶劑分子透過半透膜進入溶液或者從稀溶液進入濃溶液的自發過程稱為滲透。在一定溫度下,如果在溶液液面上施加壓力如c容器所示,是兩邊液面重新持平,這時水分子從兩邊穿過的數目完全相等,在此達到滲透平衡。如果改用同種物質的兩種不同濃度的溶液,較濃溶液的一面也不斷上升,這說明水分子透過半透膜進入溶液或者從稀溶液進入濃溶液的一面。
在醫學上把溶液中產生滲透作用的各種溶質粒子,稱為滲透活性物質。由於生物體內各部位溫度變化幅度不大,故醫學上常用滲透濃度來衡量溶液滲透壓的大小。滲透濃度就是滲透活性物質的物質的量除以溶液的體積,用符號COS表示,其常用單位也是mol/L和mmol/L,醫學上的單位是Osmol/L(滲量/升)或mOsmol/L(毫滲量/升)。1 mmol/L≈1 mOsmol/L。在計算溶液的滲透濃度時應注意,對於強電解質溶液,其滲透濃度等於溶液中溶質的離子總濃度;對於弱電解質,其滲透濃度等於溶液中未解離的非電解質分子的濃度和解離出的離子濃度的總和;而對於非電解質,其滲透濃度等於其溶液濃度。
現象解釋
滲透現象產生的原因可解釋為:由於膜的兩側水的摩爾分數不等,溶液蒸發逸出的水分子較少,即溶液的蒸氣壓小於純溶液的蒸氣壓。所以純水分子通過半透膜進入溶液的速率大於溶液中分子通過半透膜進入純水的速率,即單位時間內從純水進入溶液的水分子數要比從溶液進入純水的多。
然而隨著滲透的進行,溶液端水柱逐漸升高,水柱產生的靜水壓使得單位時間內進、出的水分子數目漸趨接近,一旦相等時,體系建立滲透平衡,此時為了阻止滲透作用進行,阻止溶劑進入溶液而必須向溶液施加的最小壓力稱為滲透壓,用符號П表示。這裡的滲透壓是用膜兩面的液面高度差所產生的壓力(F=ρgh)來量度,其數值等於滲透達到平衡時液面高度所產生的靜水壓。
有學者指出,滲透壓為維持只允許溶劑通過的膜所隔開的溶液與純溶劑之間的滲透平衡而需要的超額壓力說法不能作為定義,即無所謂施加這一說,這只是只是測定滲透壓大小的方法。溶液的滲透壓的定義應該是連通器兩邊平衡狀態下的壓差。因為滲透壓是溶液本身固有的性質之一,是通過膜指向溶液的單位面積上的力,不管是否額外施加,也不管半透膜間隔的對象溶液的另一邊溶液的濃度是多少,無論有無半透膜,它都始終存在,只是不一定表現出來,且為定值。
滲透壓定律
1866年,荷蘭物理學家范特霍夫(van't Hoff)總結大量實驗指出,在一定溫度下,難揮發非電解質溶液的滲透壓與溶質B的物質的量成正比,當濃度不變時,稀溶液的滲透壓P和熱力學溫度T成正比,比例係數為摩爾氣體常數,寫成數學式為:


當溶液很稀時,則有:

稀溶液的滲透壓和其他依數性還可以在數值上聯繫起來,即

數學推導
此時溶液中溶劑組分的化學勢與純溶劑一側的化學勢相等,滲透壓達到平衡。

假定純溶劑的摩爾體積不隨壓力變化,積分上式:

對於各組成物質在全部濃度範圍內都服從拉烏爾定律的溶液,稱之為理想溶液,此式是理想溶液的滲透壓公式。
對稀溶液有: ,式子變為:
,式子變為:


若取 ,則有
,則有


此式被稱為滲透壓公式,滲透壓的大小與溶質的量有關,而與溶質的性質無關。
套用領域
溶液的滲透壓在生物學中有很重要的作用。鮮花插在水中,可以數日不萎縮;海水中的魚不能在淡水中生活,淡水魚不能在海水中養殖,都與滲透壓有關。
植物的細胞壁有一層原生質,起著半透膜的作用,而細胞液是一種溶液,其滲透壓可高達2.0×10 Pa,土壤中水分通過這種滲透作用,送到樹梢。當植物處於水分充足的環境中,水通過半透膜想細胞內滲透,是細胞內產生很大的壓力,細胞發生膨脹,植物的根莖葉和花瓣就會有一定的彈性,這樣植物就能更好地向空間伸展職業,充分吸收二氧化碳和接受陽光。如果土壤溶液的滲透壓高於植物細胞液的滲透壓,就會造成植物細胞液內的水分向外滲透,導致植物枯萎。農業生產上改造鹽鹼地、合理施肥和施肥後及時灌水就是這個道理。

另外,人體組織內部的細胞膜、血球膜和毛細管壁都具有半透膜的性質,而人體的體液,如血液、細胞液和組織液等都具有一定的滲透壓,對病員人體靜脈輸液時,必須使用與人體血液的滲透壓相等的溶液,在310 K時,滲透壓約為7.7~7.8×10 Pa,如臨床常用的0.9%勝利鹽水和5%的葡萄糖溶液。否則有滲透作用,可以引起血球膨脹或萎縮而產生嚴重後果,右圖為紅細胞在不同濃度的NaCl溶液中的形態示意圖。當因發燒或其他原因,人體內水分減少時,血液滲透壓增高,即產生無尿、虛脫等現象,故應多飲水以降低血液的滲透壓。
毛細血管壁也是一種半透膜,隔著血漿和組織間液,它能讓低分子的水、葡萄糖、尿素、胺基酸和離子自由通過,因此,血液和組織間液間滲透壓差及水鹽平衡取決於膠體滲透壓,如果因某種原因導致血漿蛋白質減少,血漿的滲透壓降低,血漿中的水分子和其他小分子、離子就會透過毛細血管壁進入組織間液,導致血容量(人體血液總量)降低,組織間液增多,這是形成水腫的原因之一。臨床上對大面積燒傷或由於失血過多而造成血容量降低的患者進行補液時,除補以生理鹽水外,還須同時輸入血漿或右旋糖酐等代血漿,才能恢復血漿膠體滲透壓和增加血容量。
工業上常常利用滲透的對立面-反滲透來為人類服務。所謂反滲透,就是在溶液上加一個額外的壓力,如果這個壓力超過了溶液的滲透壓,那么溶液中的溶劑分子就會透過半透膜向純溶劑一方滲透,使溶劑體積增加,這一過程叫做反滲透。反滲透原理在工業廢水處理、海水淡化、濃縮溶液等方面都有廣泛套用。儘管目前成本是城市自來水生產的三倍左右,但要比用蒸餾法從海水製取淡水的能量少很多,僅為蒸餾法的30%,已成為一些海島、遠洋客輪、某些缺少飲用淡水的國家獲得淡水的方法。反滲透法處理無機廢水,去除率可達90%以上,有的竟高達99%。對於含有機物的廢水,有機物的去除率也在80%以上。作為反滲透的物質有醋酸纖維素膜、尼龍66、聚碸醯胺膜,以及氫氧化鐵、硅藻土製成的新型超過濾膜等等。
滲透壓法測定非電解質的相對分子質量尤其獨特的優點,其計算公式:


揮發性溶質溶液的依數性
要使稀溶液遵循依數性規律,溶質一定是非揮發的。但若溶質是揮發性的,又可分為下列幾種情況:
溶質揮發性大於溶劑揮發性
若溶質B是非揮發性的,此時的情況如圖1中曲些Ⅰ示。假若加入的溶質B的揮發性大於溶劑的揮發性,則溶液的蒸氣壓就應該是溶劑的蒸氣壓加上溶質的蒸氣壓,即p=p*+p(B),則溶液的蒸氣壓高於純溶劑的蒸氣壓,使得溶液的蒸氣壓在較低的溫度下達到latm。而使沸點下降為右圖中Ⅱ所示,這是因為蒸氣壓上升違反了依數性規律。例如在水中加入少量乙醇,乙醇是易揮發物質,其蒸氣壓比同溫度下的水的蒸氣壓大。因此加入乙醇,溶液的蒸氣壓增大,沸點降低,凝固點升高。

溶質揮發性小於溶劑揮發性
溶質B相對於純溶劑A揮發性較小,溶質B也可以看作是A的溶劑。當溶液為理想或對理想溶液偏差不大時,即不論溶液的濃度如何,總能符合拉烏爾定律和亨利定律,此時對溶質和溶劑的區分已無意義。對於理想液態混合物,對任一組分的蒸氣壓為:p=p*x。
pA=pA*xA,pB=pB*xB,由於溶質B的揮發性較小,pB*<pA*
pB*xB<pA*xB=pA*(1-xA)=pA*-pA*xA
pA*>pA*xA+pB*xB=pA+pB=p
其中pA、 pB分別為A 與B的分壓 ,pA*和pB*分別為A和B的飽和蒸氣壓,xA和xB為A與B的摩爾分數,p為溶液的蒸氣壓,pA*>p表明溶液的蒸氣壓必定低於純溶劑的蒸氣壓,還是符合烏拉爾定律的前提,其依數性還是蒸氣壓不斷下降和沸點不斷上升。
但在這種情況下沸點上升與溶液中溶質的質量滿足關係式 其中xB1、xB分別為氣相、液相的溶質的摩爾分數,而不是原先的線性關係。如在苯液中加入甲苯,由於甲苯相對於苯來講揮發性要小所以隨著甲苯的加入,溶液的蒸氣壓下降,沸點上升,凝固點下降,這種關係可由苯-甲苯相圖可看出。
其中xB1、xB分別為氣相、液相的溶質的摩爾分數,而不是原先的線性關係。如在苯液中加入甲苯,由於甲苯相對於苯來講揮發性要小所以隨著甲苯的加入,溶液的蒸氣壓下降,沸點上升,凝固點下降,這種關係可由苯-甲苯相圖可看出。


除此之外,沸點和凝固點的變化還可能隨著加入的溶質的量而變化,這是由於當溶質對理想溶液發生偏差所導致的。
正偏差
當溶質對理想溶液發生正偏差時,異分子間的排斥傾向起了主導作用,因而使分子更容易從溶液中逸出。相圖形狀如右圖所示,在相圖中有最低點,如圖中c點,這就決定了該類溶液的沸點變化的特殊情況,從圖中可看出A的沸點比B的沸點高,即B物質的揮發性較強。
從純淨的揮發性A物質到在C點所對應的組成的區間內,當加入相對於溶劑揮發性較強的溶質B後,溶液組分中的排斥作用不斷增強,溶液的沸點是下降的;而在C點所對應的組成到純淨的揮發性B物質的區間內,隨著溶質B的大量地加入,溶液反而顯得更加純淨,排斥作用在減弱,此時沸點是上升的。
很明顯,當加入相對於溶劑揮發性大的溶質後溶液的沸點變化恰與上述討論相反。如丙酮一CS2體系,C2H5OH一C6H6(苯)體系等的相圖即可說明。此處討論已將稀溶液擴展為溶液的範疇。
負偏差
當溶質對理想溶液發生負偏差時,組分分子間互相作用或締合,因而使分子從溶液中逸出的能力降低。體系的相圖如右圖所示。相圖中出現了最高恆沸點D點,因此D點決定了溶液沸點的變化。從圖中可看出A的沸點比B的沸點低,即A物質的揮發性較強。
從純淨的A物質到在D點對應的組成的區間內,當加入相對於溶劑揮發性較弱的溶質B後,由於組分之間的相互作用或締合作用不斷增強,溶液更加穩定,溶液的沸點升高;在D點所對應的組成到純淨的B物質區間內,加入相對於溶劑揮發性較小的物質後,沸點上升很明顯。
當加入相對於溶劑揮發性大的溶質後溶液的沸點變化恰與上述討論相反。如硝酸—水體系,丙酮—CHCl3 體系等的相圖即可說明。
電解質溶液的依數性
難揮發性非電解質稀溶液的四個依數性都能很好地符合拉烏爾定律,其實驗測定之和計算值基本相符。但電解質溶液的依數性卻極大地偏離了拉烏爾定律。電解質稀溶液依數性偏大的原因,是電解質在水溶液中能夠完全解離,是同濃度的電解質比非電解質含有更多的溶質粒子數,這種現象稱為電解質的“反常行為”,見下表。
電解質 | b(B)/(mol·kg-1) | △Tf(計算值)/K | △Tf'(實驗值)/K | i=實驗值/計算值 |
NaCl | 0.5 | 0.929 | 1.692 | 1.82 |
0.1 | 0.186 | 0.346 | 1.86 | |
0.05 | 0.0929 | 0.176 | 1.89 | |
0.01 | 0.0186 | 0.0361 | 1.94 | |
KNO3 | 0.5 | 0.929 | 1.414 | 1.52 |
0.2 | 0.372 | 0.664 | 1.78 | |
0.1 | 0.186 | 0.333 | 1.79 | |
0.05 | 0.0929 | 0.172 | 1.85 | |
0.01 | 0.0186 | 0.0359 | 1.93 | |
MgSO4 | 0.5 | 0.929 | 1.018 | 1.10 |
0.1 | 0.186 | 0.242 | 1.30 | |
0.05 | 0.0929 | 0.129 | 1.39 | |
0.01 | 0.0186 | 0.0300 | 1.61 | |
K2SO4 | 0.1 | 0.186 | 0.454 | 2.44 |
0.01 | 0.0186 | 0.0521 | 2.80 | |
MgCl2 | 0.1 | 0.186 | 0.519 | 2.78 |
參考資料來源
實驗表明,電解質稀溶液蒸氣壓下降值 、沸點上升值
、沸點上升值 、凝固點下降值
、凝固點下降值 和滲透壓
和滲透壓 ,並且存在下列關係:
,並且存在下列關係:





雖然強電解質在水中全部離解,強電解質的依數性理論上應是同濃度非電解質稀溶液的整數倍,但實驗測得電解質稀溶液的范特霍夫校正係數i並非整數。1:1型電解質如NaCl的稀溶液的i值接近於2,1:2型或2:1性電解質如MgCl2和Na2SO4等稀溶液的i則大於2而接近於3,其餘類推。且溶液越稀,i值越接近於整數。這是由於電解質在稀溶液中發生離解,而稀溶液的依數性只取決於溶質B的粒子數,而與溶質的類型無關。第一個合理解釋i值並非整數的是阿侖尼烏斯(Arrhenius)的電離理論。
電離學說
1884年瑞典化學家阿侖尼烏斯(Arrhenius)根據以上實驗事實,提出了電解質溶液的電離學說,用於解釋電解質溶液對拉烏爾定律的偏離行為。他認為電解質溶於水後可以自發解離成陰、陽兩種帶電粒子,即離子,而使溶液中溶質的粒子總數增加,導致了校正係數i總是大於1;由於正負離子不停地運動,相互碰撞時又結合為分子,所以在溶液電解質只是部分電離,電離百分數稱為電離度(degree of ionization)。
阿侖尼烏斯認為,若溶質是電解質,則其質點數將因電離而增加,所以△Tf'等依數性數值就會增大。例如0.10mol·kg-1的NaCl部分離解成Na+和Cl-,從而導致溶液中質點數增加。設電離度為α,則1kg溶劑中含有0.10(1-α)分子、αmolNa+、αmolCl-1,總共有0.10(1+α)mol的質點。
電離方程式

平衡時濃度/(mol·kg-1) 0.10(1-α) 0.10α 0.10α
因凝固點下降ΔTf都和溶液質量摩爾濃度成正比,有下列比例關係,右邊是0.10mol·kg的NaCl△Tf'/℃的計算值和實驗值。

根據電離學說,計算得到0.110mol·kg-1的NaCl只有79.3%電離成Na+和Cl-,人們將這個電離度稱為表觀電離度(apparent ionization degree),阿侖尼烏斯認為是不完全電離導致了校正係數並非是個整數。
阿侖尼烏斯還用電導法、依數性等不同的方法測定了各種電解質溶液的電離度,如下表所示,發現依數性和導電性測定值的差別已超出了實驗允許無法範圍,且濃度越大差別越大。這是因為電導法和依數法都有缺陷。電導固然與溶液里離子的多少有關,但離子的電荷、離子間的相互作用、離子遷移的速率對電導都有影響,而各種離子遷移速率都是不相同的。而依數性是將帶電子的離子和不帶電的中性分子同等看待,後來人們發現並不存在這種不帶電中性分子。
活度與離子強度
活度
雖然實驗測的強電解質的電離度小於100%,路易斯(F.M.Lewis)認為,這並不意味著強電解質中一定有未電離的分子存在。非理想溶液之所以不符合拉烏爾定律,是因為溶劑與溶質之間有相當複雜的作用,在沒有弄清這些相當複雜的作用之前,可根據實驗數據對實際濃度(x,b,c等)加以校正,並於1907年提出了有效濃度,即活度的概念,用符號α表示:

式中:γ為校正係數,稱為活度係數。因為濃度比了標準態濃度cΘ、bΘ,cΘ=1 mol·L-1,bΘ=1 mol·L-1,所以α和γ是量綱為1的數。當溶液無限稀時,離子間相互作用,可以忽略不及。此時可近似認為γ=1,即α=c/cΘ。
應當指出,用活度表示有效濃度,對非電解質的溶液,甚至對某些體系中的溶劑也可適用,活度係數γ是一個校正係數,在電解質溶液中一般是小於1的常數,但在某些特殊情況下可能大於1;在非電解質溶液中,γ可能大於1,也可能小於1。
濃度/(mol·kg-1) | HCl | KCl | NaCl | NaOH | H2SO4 | CaCl2 | CdSO4 |
0.005 | 0.928 | 0.927 | 0.929 | ---- | 0.639 | 0.785 | 0.50 |
0.01 | 0.904 | 0.901 | 0.904 | 0.89 | 0.544 | 0.725 | 0.40 |
0.05 | 0.830 | 0.815 | 0.823 | 0.82 | 0.340 | 0.57 | 0.21 |
0.10 | 0.796 | 0.769 | 0.778 | 0.776 | 0.265 | 0.524 | 0.17 |
0.20 | 0.767 | 0.718 | 0.735 | 0.757 | 0.209 | 0.48 | 0.137 |
0.50 | 0.757 | 0.649 | 0.681 | 0.735 | 0.154 | 0.52 | 0.067 |
1.00 | 0.809 | 0.604 | 0.657 | 0.757 | 0.130 | 0.71 | 0.041 |
2.00 | 1.011 | 0.576 | 0.670 | 0.70 | 0.124 | 1.55 | 0.035 |
3.00 | 1.32 | 0.571 | 0.710 | 0.77 | 0.141 | 3.38 | 0.036 |
4.00 | 1.76 | 0.597 | 0.791 | 0.89 | 0.171 | --- | --- |
參考資料來源
然而,在電解質溶液中,正負粒子總是同時共存,實際上無法用實驗方法測定單種離子的活度,為此有引入了平均活度的概念。其定義式為 :

對於化學式為AxBy的強電解質溶液來說, 與b的關係為:
與b的關係為:


式中, 離子平均質量摩爾濃度。
離子平均質量摩爾濃度。 稱為離子平均活度係數。它可用多種實驗方法測定。它的大小不僅與離子的濃度有關,還和離子的電荷相關。實驗結果表明,離子電荷對活度的影響比離子濃度還要大些。
稱為離子平均活度係數。它可用多種實驗方法測定。它的大小不僅與離子的濃度有關,還和離子的電荷相關。實驗結果表明,離子電荷對活度的影響比離子濃度還要大些。


離子強度
路易斯於1921年提出離子強度的概念,表示離子電荷和離子濃度這兩個因素對活度係數的影響:

式中:I為離子強度,c(B)和Z(B)分別為組分B的濃度(包括x,b,c等)和電荷數。顯然離子濃度越大,離子電荷越高,離子強度越大。
如計算0.050mol·L-1AlCl3溶液中的離子強度。

強電解質理論
強電解質在水中是完全離解的,在溶液中的粒子濃度很大。由於離子間存在較強的靜電引力,對某一正離子來說,必然吸引負離子而排斥正離子,使其周圍聚集較多的負離子和較少的正離子,即在正離子周圍形成一個負離子的包圍圈,稱為離子氛(ion atomosphere),由於離子氛的存在,溶液中的粒子相互牽制,離子的運動不能完全自由,是粒子在溶液中遷移速度減慢。相當於離子減少,電離度降低。
此外,人們還發現,在強電解質溶液中不但有離子氛存在,而且帶相反電荷的離子鍵還能相互締合成“離子對”,1926年提出的卜耶隆離子締合理論,認為在溶液中凡是異號電荷離子間靜電吸引能超過2kT,靜電能大於熱運動能時,即可形成離子對。如Na+Cl-,在溶液中作為一個整體運動,比較穩定,就像一個電中性分子。
由於“離子氛”和“離子對”的影響,強電解質溶液的依數性都比完全離解的理論計算值小,溶液越濃或離子價數越高,這種偏差就越大。
德拜-休克爾極限公式
離子平均活度係數 與離子強度I有關
與離子強度I有關



如計算25°C時,計算0.01mol·kg-1的NaCl溶液中,離子的平均活度係數和離子的平均活度 。
。





德拜-休克爾公式
下式為德拜-休克爾公式,可以計算單個離子的的活度係數,適用在稀溶液(c<0.Imol·L-1):

其中B、a為常數,Zi為離子的電荷;I為溶液的離子強度。
如計算0.050mol·LAlCl3溶液中Cl-1和Al3+的活度係數並由此計算活度。已知Cl-1的a=300,Al的a=900,b=0.00328,I=0.30mol·L-1。由德拜-休克爾公式:


由此可以看出同樣的離子強度,對高價離子影響大,其離子活度a會極大地下降。


套用領域
電解質溶液依數性的套用也有很多。例如,工業上或實驗室中常採用某些一潮解的固態物質如CaCl2、P2O5等作為乾燥劑,其乾燥原理是蒸氣壓下降:固態物質潮解後在其表面形成飽和溶液,由於溶液濃度較大,其蒸氣壓較低,當空氣中水蒸氣的分壓大於溶液的蒸氣壓時,空氣壓重的水蒸氣就會不斷地進入溶液,使固態物質不斷潮解,直到固體物質完全溶解或氣液兩相的蒸氣壓相等為止。
利用溶液凝固點下降這一性質,冬季可撒鹽除雪,當食鹽或氯化鈣與冰(或雪)接觸時,在食鹽或氯化鈣的表面形成極濃的鹽溶液,而這些濃鹽溶液的蒸氣壓比冰(或雪)的蒸氣壓低得多,冰(或雪)則以升華或熔化的形式進入鹽溶液。進行上述過程都要吸收大量的熱,從而使體系的溫度降低。利用這一原理,可以自制冷凍劑。一份食鹽和三塊冰混合,體系的溫度可降至-20℃,10份六水氯化鈣與7~8份碎冰均勻混合,體系的溫度降至-40~-20℃。用CaCl2、冰和丙酮的混合物,可以致冷到-70C°以下。
| 鹽 | 質量/g | 冰鹽點/℃ |
|---|---|---|
KOH | 47.1 | -65.0 |
ZnCl2 | 108.3 | -62.0 |
CaCl2·6H2O | 143.0(125.0) | -55.0(-40.3) |
NaCl | 33 | -21.2 |
NaNO3 | 59 | -18.5 |
NH4Cl | 25 | -15.8 |
KCl | 30 | -11.0 |
CaCl2 | 80 | -11.0 |
參考資料來源
濃溶液的依數性
濃溶液由於存在著更為複雜的情況,導致其依數性與理想情況偏離較為嚴重,所以依數性跟計算值有差異。但依然認為其具有依數性的。高濃度使得溶質粒子之間的相互影響大為增加,簡單的依數性的定量關係不再適用。
溶劑化
這是因為溶液中溶質粒子是溶劑化的,溶劑化程度的大小與粒子種類、溶液濃度、溫度等因素有關;液體的結構是最複雜的。 液體與氣體一樣具有流動性, 但具有體積這一點卻與固體相似。由液體的流動性可知, 它與氣體一樣粒子間相對運動激烈, 因此粒子的排列不規則; 從它的密度接近固體這一點看, 又不象氣體那樣紊亂。據X-射線研究已知: 液體不是完全無規則, 而具有某種程度的與結晶性固體相似的有規則的分子排列, 其規律性離中心分子僅有幾個分子程度。且已明確了其排列只限於短程式,而不象晶體那樣的長程式。 可見: 溶劑分子間往往是締合的, 而不是單個的“質點”。締合程度的大小與溶劑的種類和溫度有關。
粒子半徑
拉烏爾定律未考慮溶質和溶劑粒子的大小差別。首先, 由於溶劑分子間始終存在著締合與解離之間的動態平衡, 每個“ 溶劑粒子”( 指同締合程度的溶劑分子的混合物)的大小就不同了。這種因締合程度不同引起的“ 溶劑粒子”大小的差別是動態變化的、難以準確測定的。其次, 不同溶質粒子本身大小差別很大。 從鮑林推算出的一些常見離子半徑以看出, 即使是單原子離子的半徑差別也可高達數倍。葡萄糖、蔗糖、環糊精等多原子分子由於有數十個甚至上百個原子組成, 其半徑必然是水分子等小分子半徑的數倍。 高分子化合物溶液中的溶質與溶劑分子的半徑差別可達數十倍甚至上百倍。 這種粒子大小的差別是不可忽略的。第三, 由於溶劑化作用的存在, 同一溶液在不同濃度和溫度下溶質粒子的溶劑化程度不同, 粒子大小也就不同了。當濃度一定時, 溫度升高則每個溶質粒子的溶劑化程度減小; 當溫度一定時, 濃度增大則每個溶質粒子的溶劑化程度減小。 而且由於分子的熱運動, 每個溶質粒子的溶劑化程度的大小是動態變化的。
分子極性與范德華力
所以,此時依數性的定義中說與“溶質的本性無關”就不對了。



