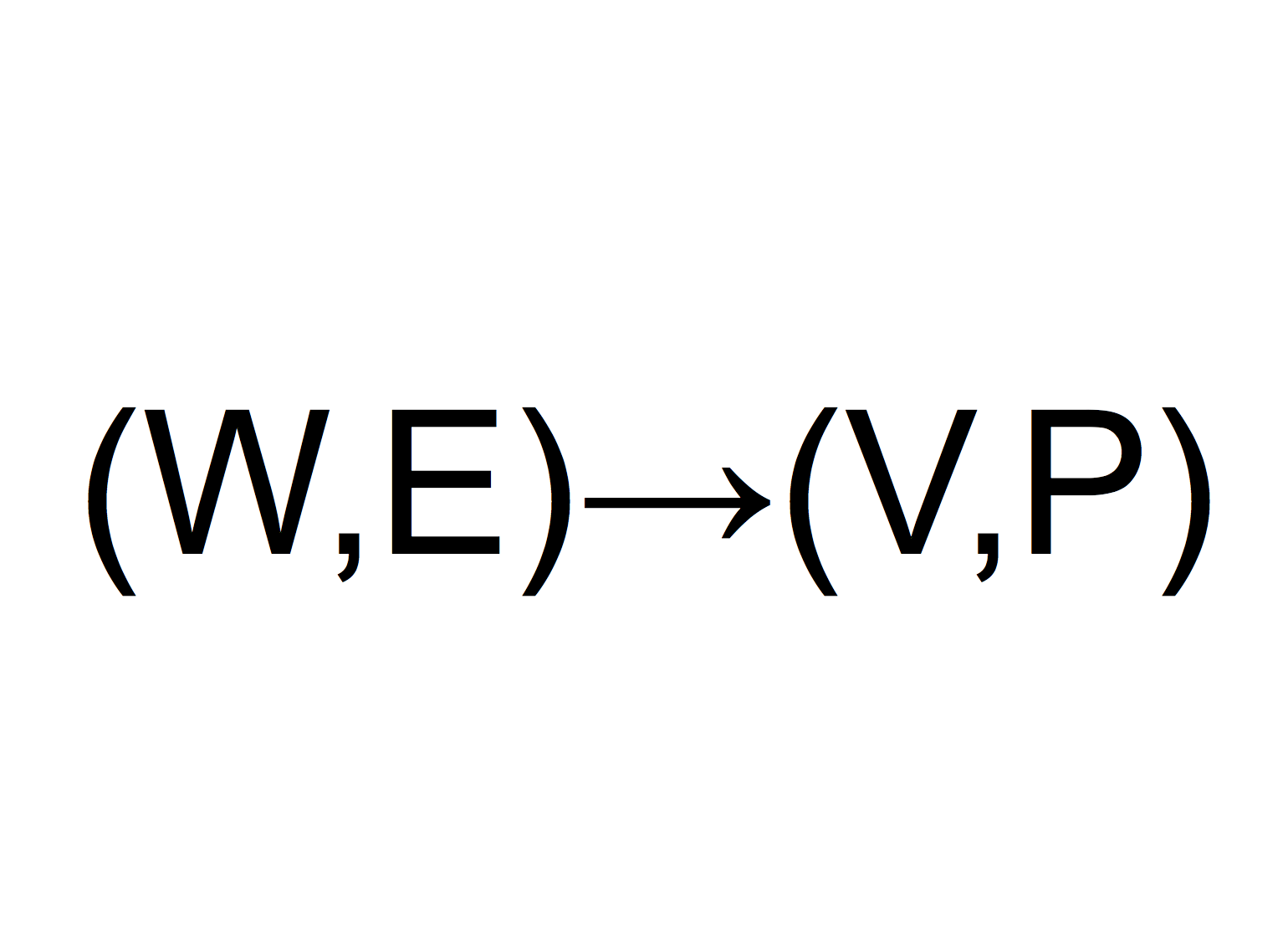基本介紹
- 中文名:例外曲線
- 外文名:exceptional curve
- 適用範圍:數理科學
簡介,例外子簇,定義,套用,
簡介
代數曲面上的例外除子稱為例外曲線(exceptional curve)。
例外子簇
定義
[exceptional subvariety]
代數閉域上代數簇X的閉子簇Y滿足: 存在雙有理態射f:X→X1, Y在f下的像Y1是維數較小的子簇,並且f:X\Y→X1\f(Y)是同構。態射f稱為Y到Y1=f(Y) 上的收縮(contraction)。如果X,X1,Y,Y1是光滑不可約簇,則稱Y為第一類例外子簇(esceptional subvariety of the first kind)。如果Y在X中的余維數是1,則稱Y是例外除子(exceptional disvisor)。
套用
例外子簇的概念能自然地推廣到概形,代數空間和復解析空間上。對應態射稱為收縮(contraction)。也能自然地推廣第一類例外子簇的概念,復解析空間中的例外子簇亦稱例外解析集(exceptional analytic set)。
刻畫例外子簇是雙有理幾何學的基本問題之一,歷史上第一個這樣的刻畫的例子是恩里克斯-卡斯泰爾諾沃準則(Enriques–Castelnuovo criterion):光滑曲面X上不可約完全曲線Y是第一類例外子簇,若且唯若Y同構於射影直線P1,且Y在X上的自交數(Y·Y) 等於-1。這個準則能推廣到二維正則概形的一維子概形上。如果 是光滑射影曲面X上具有不可約分支Yᵢ的任意連通完全曲線,則Y是例外除子的必要(但不充分) 條件是矩陣(Yᵢ·Y𝗃) 是負定的。在光滑復曲面上的連通復曲線,或者二維光滑代數空間上的連通完全曲線的情形,刻畫例外子簇的類似條件是充分必要的。
是光滑射影曲面X上具有不可約分支Yᵢ的任意連通完全曲線,則Y是例外除子的必要(但不充分) 條件是矩陣(Yᵢ·Y𝗃) 是負定的。在光滑復曲面上的連通復曲線,或者二維光滑代數空間上的連通完全曲線的情形,刻畫例外子簇的類似條件是充分必要的。

在代數空間的情形下,例外性的最一般的準則是:在諾特代數空間的範疇中,X的子空間Y是例外子簇,若且唯若在形式代數空間的範疇中,形式完全化Y在X中是例外子簇。換句話說,代數子空間能收縮,若且唯若與之對應的形式完全化也能收縮。