定義
位置度解釋
位置度 是多種形位公差形狀和位置公差中的一種。如此一來這個“位置度”一詞就好理解了。 它的意思是被標註對象在實際物體上的位置所允許出現的
誤差範圍。 如以上面所寫意思為以A,B,C三個面為基準面 標準平面要保證所標註的物體與三個面之間的位置誤差不得超過0.1。 而有φ者是說
偏差是在一個圓面的範圍內而不帶的則是表示直線上的偏差為多少。
公差帶
位置度公差帶是一以理論位置為中心對稱的區域。
點的位置度:公差帶是直徑為公差值t的球內的區域,球公差帶的中心點的位置由理論正確尺寸確定。
線的位置度:公差帶是直徑為公差值t的圓柱面內的區域,公差帶的軸線的位置由理論正確尺寸確定。
三要素
1、基準﹔
2、理論位置值﹔
3、位置度公差。
公差注法
基本原則
位置度公差是各實際要素相互之間或它們相對一個或多個基準的位置所允許的變動全量。
在位置度公差注法中,用理論正確尺寸和位置度公差限定各實際要素相互之間和(或)它們相對一個或多個基準的位置。位置度公差帶相對於理想位置為對稱公布。
位置度公差可以用於單個的被測要素,也可以用於成組的被測要素,當用於成組被測要素時,位置度公差帶應同時限定成組要素中的每個被測要素。
正確注法
在位置度公差注法中,理論正確尺寸是確定被測要素理想位置的尺寸,該尺寸不直接附帶公差。
幾何圖框是確定一組被測要素之間的理想位置和(或)它們與基準之間正確幾何關係的圖形。
標註時,應根據零件的功能要求,選用下列的理論正確尺寸注法。
確定成組要素中各要素之間的理想位置關係:
若成組要素中的各要素在
圓周上均勻分布時,各要素間的理論正確角度允許省略不注,在公差框格上方加注“均布”兩字(圖4)。此時,各要素間的角向位置關係為圓周理想等分的角度關係。
c. 採用混合法(圖5)。
d. 採用表格注法(圖6)。
圖1至圖6中各理論正確尺寸僅確定成組要素組內各要素(孔的軸線)相互間的理想位置關係,在圖中分別用相應的幾何圖框表示。
確定各要素之間及相對基準的理想位置關係:
a. 採用直角坐標法(圖7至圖9)
圖7中基
準線A作為確定各條被測線理想位置的尺寸起始線。
圖8中基準平面A、B構成的互相垂直的基準體系作為確定各孔理想位置的坐標尺寸起始面。
有對中心基準要求的要素,其理論正確尺寸應從基準中心平面注起(圖9)。
圖9中基準中心平面A確定了孔組的定位和定向要求。
b. 採用極坐標註法(圖10)。
圖10中基準軸線A確定四孔孔組幾何圖框的中心位置;基準中心平面B確定孔組幾何圖框的角向理想位置。
註:由於理論正確尺寸不直接附帶差,因此,無論採用何種形式的理論正確尺寸注法(鏈式或同一基準式),均不會產生公差累積。
選擇方法
在位置度公差標註中,公差標註給出允許實際要素偏離其給定理想位置的變動區域(即公差帶)。根據零件功能要求,選用下列的一種公差注法。
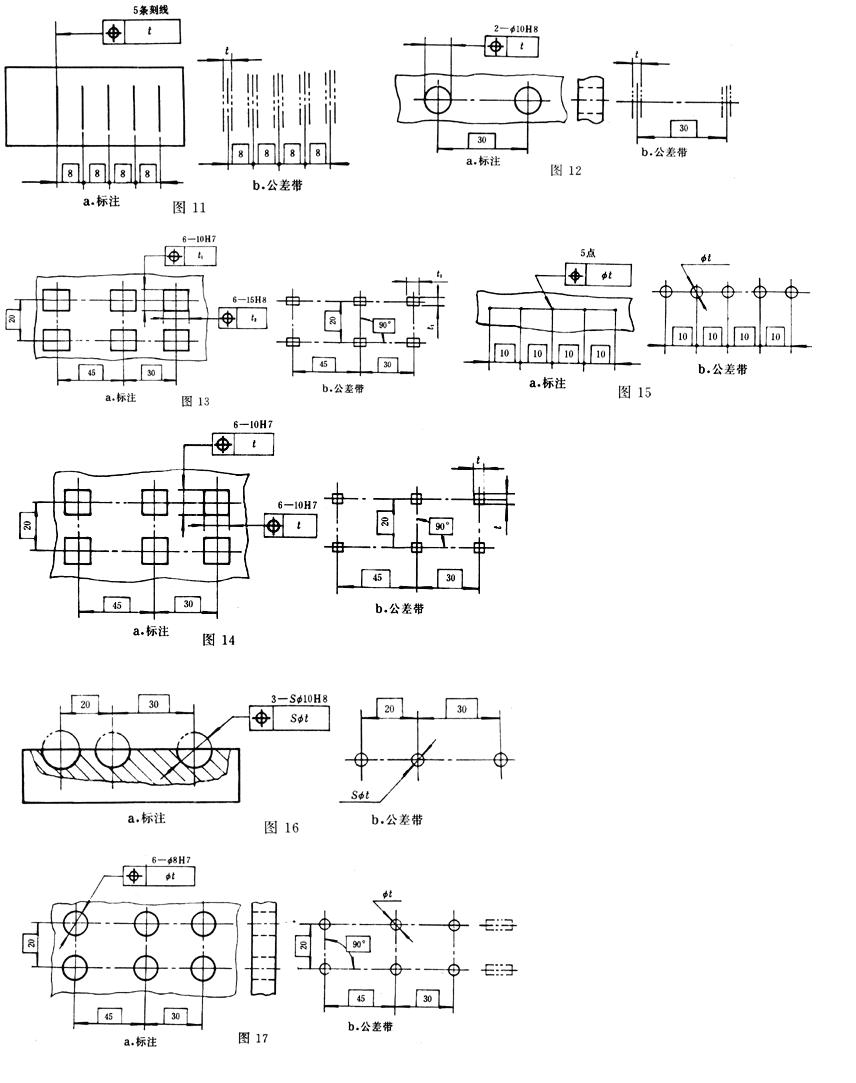
1、在給定方向上
當僅在一個方向上給定位置度公差時,公差帶是距離為公差值t,且以理想位置為
中心對稱配置的兩平行直線(或兩平行平面)之間的區域,見圖11和圖12。此時,公差帶的寬度方向是框格指引線箭頭所指的方向。
當在兩個方向上給定位置度公差時,公差帶是正截面為公差值t1×t2,且以理想位置為軸線的
四稜柱內的區域。
a. 兩個方向給定不相等的公差值(t1≠t2)(圖13)。
b. 兩個方向給定相等的公差帶(t1=t2=t)(圖14)。
2、在任意方向上
當在任意方向上給定位置度公差時,公差帶是直徑為公差值t,且以理想位置為中心(或軸線)的圓、球(或
圓柱)內的區域(圖15至圖17)。
a. 平面上點的任意方向(圖15)。
b. 空間點的任意方向(圖16)。
c. 軸線的任意方(圖17)。
基準注法
在位置度公差標註中,基準用於確定圖形中被測要素的方向或(和)位置。應根據功能要求,選用不同類型的基準,確定
理想要素(或幾何圖框)的方向或(和)位置。
1、注出一個基準
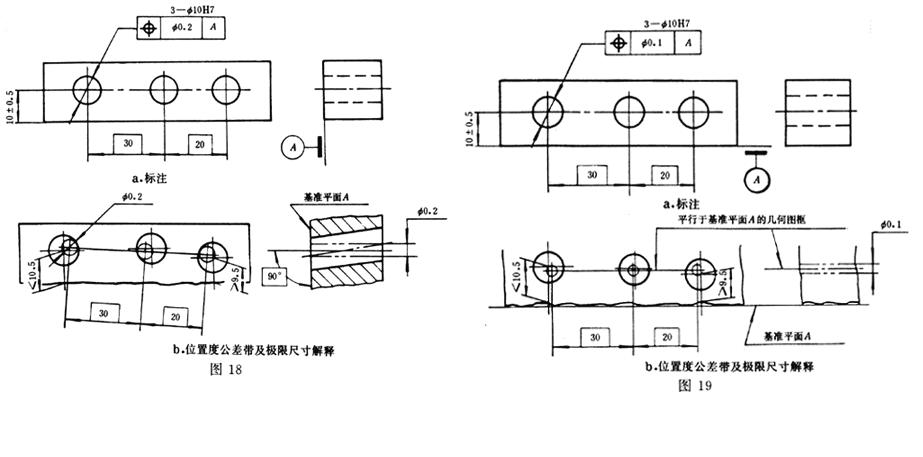
注出一個基準確定理想要素(或幾何圖框)的方向(圖18和圖19)。
a. 確定垂直關係(圖18)
圖18中基準平面A用來確定三孔孔組幾何圖框相對端面的垂直關係。此時,幾何圖框的軸線應垂直於基準平面A。各孔軸線距底邊的尺寸應位於9.5mm至10.5mm之間。
b. 確定平行關係(圖19)
圖19中基準平面A確定三孔孔組
幾何圖形相對底邊的平行關係。此時,幾何圖框可平行於底邊上下浮動。各孔軸線距底邊的尺寸應位於9.5mm至10.5mm之間。
註:用基準確定幾何圖框的方向時,圖18a中的90°和圖19a中的平行關係可以省略不注。
注出一個基準確定理想素(或幾何圖框)的位置(圖20至圖22)。
a. 輪廓基準(圖20)
圖20中基準平面A確定兩個孔在垂直方向上的理想位置。
b. 中心要素基準(圖21)。
圖21中基準軸線A確定兩個φH7孔的理想位置。
c. 圓周方向基準(圖22)
圖22中基準中心平面A確定五孔孔組幾何圖框在圓周方向的理想位置。
2、注出三基面體系
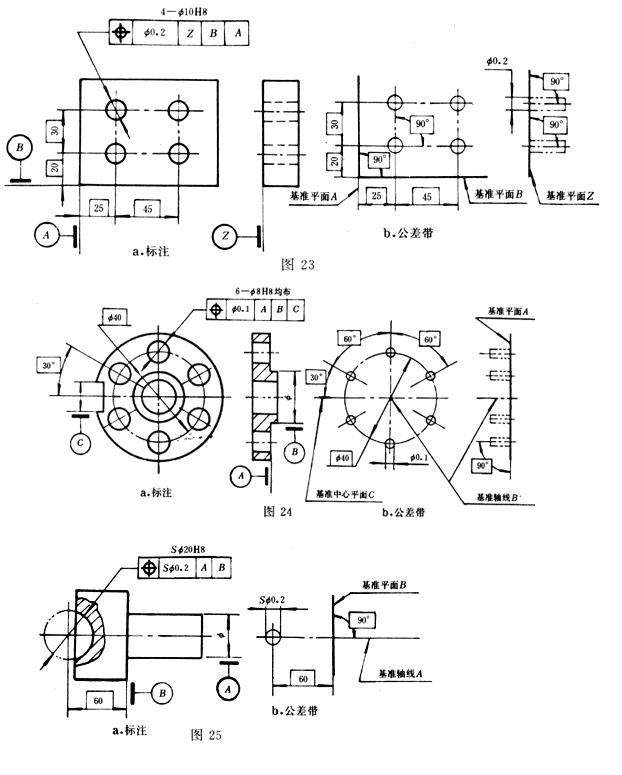
三基面體系是由三個互相垂直的基準平面組成的基準體系。在位置公差標註中,可採用三基面體系確定要素的理想位置。
圖23中由基準平面Z、B、A構成的三基面體系確定四個孔的理想位置。
圖24中由基準平面A和基準軸線B級成的三基面體系確定圓周均勻分布六個孔的理想位置;基準中心平面C確定圓周分布六個孔的角向位置。
圖25中由基準線A和基準平面B克成的三基面體系確定球心的理想位置。
3、注出成組要素基準
在位置度公差標註中,可注出成組要素構成的基準(圖26a)。
在圖26中,四孔孔組與外側邊有功能關係,以基準平面A、B構成的基準體系確定四孔孔組的理想位置關係;而八孔孔組與四孔孔組有直接的功能關係,故以四孔孔組幾何圖框的中心位置(D基準)為基準。
基準中心D的建立方法如下:
a. 用具有孔組內理想位置關係(與基準平面A、B的理論正確尺寸無關)的四個
圓柱面分別包容各實際軸線;
b. 同進逐步縮小四個包容圓柱面的趕緊徑,且四孔孔組幾何釁框可平移或轉動,使包容面的直徑為最小;
c. 包容面直徑為最小時的幾體何圖框中心為基準中心D(圖26C)。
公差注法
1、採用關聯包容原則的位置度公差注法
當位置度公差採用關聯包容原則時,應在公差格內採用“0 ”形式標註(圖27a)。
在圖27中,四個孔的實際輪廓必須分別遵守直徑為10mm(孔的最大實體尺寸)的四個關聯最大實體邊界,各最大實體邊界的軸線必須保持圖樣給定的幾何圖框關係(圖27b)。
2、採用最大實體原則的位置度公差注法
當位置度公差採用最大實體原則時,應在公差框格中標註符號“ ”(圖28a)。
在圖28中,四個孔的實際輪廓必須分別遵守直徑為9.9mmA(孔的實效尺寸)的四個關聯實效邊界,各實效邊界的軸線必須保持圖樣給定的幾何圖框關係(圖28b)。
3、基準要素採用最大實體原則的位置度公差注法
在位置公差採用相關原則時,其基準要素也可以根據需要採用最大實體原則,其標註方法為在相應的基準字母之後加注符號“ ”(圖29a和圖30a)。此時基準要素的理想邊界由基準要素自身所採用的
公差原則來確定。
在圖29中,基準孔A本身要求遵守單一包容原則,因此其實際輪廓必須遵守直徑為35mm(基準孔的最大實體尺寸)的單一最大實體邊界,該邊界的軸線作為兩孔孔組的基準,確定兩個被測實效邊界的位置(圖29b)。
在圖30中,
基準台階本身要求遵守關聯最大實體原則,因此,其實際輪廓必須遵守必須遵守趕緊徑為φ60.10mm(台階的實效尺寸)的關聯實效邊界,端面B與該邊界的軸線構成三基面體系,確定八個被測實效邊界的位置(圖30b)。
註:位置度公差採用相關原則後,其量規的設計方法參見GB 80659《位置量規》。
複合注法
1、尺寸公差和位置度公差的複合注法
如果一組要素相互之間的關係用位置度公差標註,而整組要素又由
線性尺寸公差定位(圖31a),則應獨立地分別滿足各筇睚的要求。
四個孔的實際軸線必須分別位於直徑均為公差值0.01mm的四個圓柱形位置度帶內,各個位置度公差帶相互間應具有理想位置關係(圖31b)。
左側兩個孔的實際軸線與左側邊之間的距離應位於極限位於極限尺寸17.9mm和18.1mm之間(用兩點法測量,見GB 4249)。
底下兩個孔的實際軸線與底邊之間的距離應位於極限尺寸19.9mm和20.1mm之間(圖31c)。
如果一組要素相互間的位置關係用位置
公差標註,而整組要素由角度公差定位(圖32a),則應獨立地分別滿足各自的要求。
圖32中四個孔的實際思線必須分別位於直徑均為公差值0.1mm的四個圓柱形位置度公差帶內,位置度公差帶相互間應具有理想位置關係,且幾何圖框應與基準軸線A同軸(圖32b)。
左上孔的軸線和槽中心平面與A孔思線的連線之間的角度應該位於44°30`和45°30`之間(圖32c)。
2、複合位置度公差注法
如果一組
要素內各要素相互之間的位置度關係用位置度公差標註,整組要素相對其他要素也用位置度公差定位,則兩個位置度公差應分別滿足。
對同一組要素給定的複合位置度公差,其標註可由上、下兩個框格組成;上框格給出整組要素的定位公差,下框格給出一組要素內,各要素相互之間的位置公差。
圖33中四個孔的實際軸線必須分別位於直徑均為0.01mm的四個圓柱形公差帶內。各位置度公差帶應位於相互間的理想位置上,並垂直於基準平面A(圖33b)。
四個孔的實際軸線還必須分別位於直徑均為0.2mm的四個圓柱形公差帶內,各位置度公差帶應位於相對基準A、Y、Z和相互間的理想位置上(圖33c)。
圖34中六個孔的實際軸線必須分別位於直徑均為0.01mm的六個圓柱形公差帶內,各位置度公差帶應位於相互間的理想位置上,並垂直於基準平面A(圖35b)。
六孔的實際
軸線還必須分別位於直徑均為0.2mm的六個圓柱形公差帶內,各位置度公差帶應位於相對基準A、B、C和相互間的理想位置上(圖34c)。
位置度誤差分類
位置誤差根據其位置,可以分為以下三類:
定向誤差:平行度、垂直度和傾斜度
定位誤差 :位置度、同軸度和對稱度
跳動:圓跳動、全跳動
1、定向誤差
定義:是被測實際要素對一具有確定方向的理想要素的變動量,該理想要素的方向由基準確定。
意義:定向誤差值用定向最小包容區域(簡稱定向最小區域)的寬度或直徑表示。定向最小區域是指按理想要素的方向包容被測實際要素時,具有最小寬度或直徑的包容區域。理想要素首先要與基準平面保持所要求的方向,然後再按此方向來包容實際要素,所形成的最小包容區域,即定向最小區域。
定向公差具有如下特點:
1) 定向
公差帶相對基準有確定的方向,而其位置往往是浮動的。
2) 定向公差帶具有綜合控制被測要素的方向和形狀的功能。
因此在保證功能要求的前提下,規定了定向公差的要素,一般不再規定形狀公差,只有需要對該要素的形狀有進一步要求時,則可同時給出形狀公差,但其公差數值應小於定向公差值。
2、定位誤差
定義:是被測實際要素對一具有確定位置的理想要素的變動量,該理想要素的位置由基準和理論正確尺寸來確定。
意義:定位誤差值用定位最小包容區域(簡稱定位最小區域)的寬度或直徑表示。定位最小區域是指以理想要素定位來包容被測實際要素時,具有最小寬度或
直徑的包容區域。
定位公差帶的特點如下:
1) 定位公差相對於基準具有確定位置。其中,位置度公差帶的位置由理論正確尺寸確定,同軸度和對稱度的理論正確尺寸為零,圖上可省略不注。
2) 定位公差帶具有綜合控制被測要素位置、方向和形狀的功能。
在滿足使用要求的前提下,對被測要素給出定位公差後,通常對該要素不再給出定向公差和形狀公差。如果需要對方向和形狀有進一步要求時,則可另行給出定向或形狀公差,但其數值應小於定位公差值。
3、跳動
它可分為圓跳動和全跳動。
圓跳動:是指被測實際表面繞基準
軸線作無軸向移動的迴轉時,在指定方向上指示器測得的最大讀數差。
全跳動:是指被測實際表面繞基準軸線無軸向移動的迴轉,同時指示器作平行或垂直於基準軸線的移動,在整個過程中指示器測得的最大讀數差。
跳動是某些形位誤差的綜合反映。
差值計算
本章給出適用於呈任何分布形式的內、外相配要素,為保證裝配互換而給定位置度公差的公差值計算方法。
1、代號
t--位置度公差值(公差帶的直徑或寬度)
S--光孔與緊固件之間的間隙
Dmin--光孔的最小直徑
K--間隙利用係數
2、螺栓連線的計算方式
2.1 用螺栓連線兩個或兩個以上的零件,且被連線零件均為光孔,其孔徑大於螺栓直徑,如圖45。
式中:S=Dmin-dmax
K的推薦值為:
不需調整的連線:K=1;
需要調整的連線:K=0.8或K=0.6。
註:K值的選擇應根據連線件之間所需要的調整間隙量確定。
例如:某個採用螺栓連線的部位,其光孔與緊固件之間的間隙為1mm:
a. 若設計只要求裝配時螺栓能順利地穿入被被連線件的光孔,各被連線件不需作相互錯動的調整;此時,選K=1,則t=1mm。若被連線件光孔的位置度誤差達到最大值1mm,螺栓穿入後,被連線件之間無法相互錯動調整。
b. 若設計要求在螺栓穿入被連線件的光孔後,為保證其他環節的調整需要,如邊緣對齊等,各被連線件之間應能相互錯動調整0.4mm,此時,選K=0.8,則t=0.8mm。若被連線件光孔的位置度誤差均達到最大值0.8mm,螺栓穿入後,兩被連線件之間仍有0.4mm的相互錯動調整量。
2.2 若考慮結構,加工等因素,被連線零件採用不相等的位置度公差ta、tb時,則應滿足:ta+tb≤2t。
若連線三個或更多個零件而採用不相等的
位置度公差時,則任意兩個零件的位置公差之和應滿足:ta+tb≤2t。
3、螺釘(或螺柱)連線的計算公式
3.1 被螺釘(或螺柱)連線的零件中,有一個零件的孔是螺孔(或過盈配合孔),而其它零件的孔均為光孔,且孔徑大於螺釘直徑,如圖46。
式中:S=Dmin-dmax
K的推薦值為:
不需調整的連線:K=1;
需要調整的連線:K=0.8或K=0.6。
3.2 若考慮結構、加工等因素,被連線
零件採用不相等的位置度公差ta、tb時,則螺孔(或過盈配合孔)與任一零件一位置公差組合必須滿足:ta+tb≤2t。
4、位置度公差值數系
按以上公式計算確定的位置度公差,以化整後按下表選擇標準公差值。
位置度公差值數系
1
| 1.2
| 1.5
| 2
| 2.5
| 3
| 4
| 5
| 6
| 8
|
1×10
| 1.2×10
| 1.5×10
| 2×10
| 2.5×10
| 3×10
| 4×10
| 5×10
| 6×10
| 8×10
|
5.、當採用
螺釘連線時,如螺孔(或過盈配合孔)的垂直度誤差影響較大時,則以上公式不能保證自由裝配。此時,為了保證自由裝配的要求,螺孔(或過盈配合孔)的位置度公差可採用“延伸公差帶”。