仿微分運算元(para-differential operator)現代偏微分方程理論中一類很重要的運算元,是擬微分運算元的一種推廣。仿微分運算元理論是擬微分運算元理論的某種延伸,它們之間有許多相似及借鑑之處。
基本介紹
- 中文名:仿微分運算元
- 外文名:para-differential operator
- 套用學科:數學術語
- 範疇:數理科學
- 涉及:運算元
- 同類:擬微分運算元
概念



























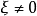




基本原理




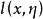















仿微分運算元(para-differential operator)現代偏微分方程理論中一類很重要的運算元,是擬微分運算元的一種推廣。仿微分運算元理論是擬微分運算元理論的某種延伸,它們之間有許多相似及借鑑之處。



























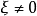








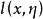














仿微分運算元(para-differential operator)現代偏微分方程理論中一類很重要的運算元,是擬微分運算元的一種推廣。仿微分運算元理論是擬微分運算元理論的某種延伸,它們之間有許多...
仿微分運算元象徵(symbols of paradifferen-tial operators)確定仿微分運算元的一個映射,它是一個線性連續滿映射.由定義...
《仿微分運算元引論》是1990年科學出版社出版的圖書,作者是陳恕行、仇慶久、李成章。...... 《仿微分運算元引論》是1990年科學出版社出版的圖書,作者是陳恕行、仇慶久、...
現代微分運算元理論是20世紀50年代,由米赫林、考爾德倫(Calderon,A.P.)和贊格蒙(Zygmund,A.)等人發展起來的奇異積分運算元理論。...
本書的結構大體上是:第二、三、四章主題是非線性微局部分析,包括J.-M.Bony所創立的仿微分運算元理論以及非線性奇性分析。後三章包括了非齊性Sobolev空間上的擬...
非線性運算元運算元的微分學 編輯 從分析上研究一般運算元的途徑是把數學分析中研究函式的微積分學推廣到運算元。設X、Y都是B空間,U是X中的一個開集,ƒ:U→Y,稱...
同倫運算元(homotopy operator)是具有同倫性質的線性變換。 兩個拓撲空間X和Y同...同倫運算元微分流形 編輯 設M是仿緊豪斯道夫 (Hau-sdorff)空間,且是拓撲流形...
實係數微分奇異同調群(differential singularhomology group with real coefficients)是邊緣運算元誘導的線性變換的核關於其像的商空間。對於每個p≥0,設∞Sp(M,R)表示...
仿積(paraproduct)是將乘積uv化為線性部分與光滑性更高的函式之和的一種運算元。...... 是可以一一映射的,所以取機率符號P,認為也是一個運算元,和微分,積分運算元運算元...
1981.01 《偏微分方程概論》 陳恕行編 北京:人民教育出版社 1988.07 《偏微分方程近代方法》 陳恕行,洪家興編著 上海:復旦大學出版社 1990.02 《仿微分運算元引論》...
2.Gevrey類上的非線性微局部分析理論:在非線性微局部分析方面,將Bony的仿微分運算元理論推廣到了Gevrey類,並在所建立的框架下證明了非線性方程的微局部亞橢圓性以及...
用》、《仿微分運算元引論》及論文20多篇。詞條標籤: 人物 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:2次歷史版本 最近更新: 創建者:joux19...
1.2擬微分運算元和Fourier積分運算元 1.3 Bony的仿微分分解及其套用 1.4 FBl變換和Wigner變換 參考文獻 2幾何中幾個定理的欣賞 2.1勾股定理Euclid幾何 2....
微局部分析是偏微分方程運算元理論中的一個重要的研究領域。在擬微分運算元及傅立葉積分運算元理論中,常將所論問題化為對相應的象徵(及位相)的處理。實際上,現代微分...
