亨澤爾賦值(Henselian valuation)是一種特殊的賦值。指域F上的賦值,它在F的任何代數擴張上都只有惟一的拓展。此時,對應的賦值環滿足亨澤爾條件。亨澤爾賦值在研究多項式分解中有重要作用。
基本介紹
- 中文名:亨澤爾賦值
- 外文名:Henselian valuation
- 領域:數學
- 學科:域論
- 性質:一種特殊的賦值
- 提出者:亨澤爾
代數擴張
環
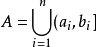
亨澤爾賦值(Henselian valuation)是一種特殊的賦值。指域F上的賦值,它在F的任何代數擴張上都只有惟一的拓展。此時,對應的賦值環滿足亨澤爾條件。亨澤爾賦值在研究多項式分解中有重要作用。
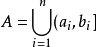
亨澤爾賦值(Henselian valuation)是一種特殊的賦值。指域F上的賦值,它在F的任何代數擴張上都只有惟一的拓展。此時,對應的賦值環滿足亨澤爾條件。亨澤爾賦值在研究...
將某一數值賦給某個變數的過程,稱為賦值。將確定的數值賦給變數的語句叫做賦值語句。各程式設計語言有自己的賦值語句,賦值語句也有不同的類型。所賦“值”可以是...
亨澤爾引理(Hensel's Lemma )代數數論中的一個重要定理.由多項式在剩餘類域上的分解得出其在完備域上分解的定理.設域F,對非阿基米德賦值甲完備,O為賦值環,P為...
亨澤爾條件(Henselian condition)一種與亨澤爾賦值環等價的條件.設B是局部環,MB是它的極大理想,F=B/MB是它的剩餘域,n是從B到F的正規同態映射(即對於每個bEB,...
亨澤爾域亦稱亨澤爾賦值域一種重要的賦值域。...... 亨澤爾域[1] (Henselian field)亦稱亨澤爾賦值域一種重要的賦值域.若φ是域F的一個亨澤爾賦值,則稱賦值域(F...
亨澤爾化(Henselization)賦值域的最小亨澤爾擴張.設(K,φ)是賦值域(F,φ)的一個賦值擴張,若滿足下列條件,則稱(K,φ)是(F,φ)的一個亨澤爾化:1. (K,φ...
這一工作導致賦值論以及局部域理論的 發展。他也是哈塞原理最早的奠基者,他的學生H.哈塞 發展了□ 進理論。亨澤爾和哈塞的“局部-整體原理” 著稱於世。亨澤爾...
可許亨澤爾擴張(allowable Henselian exten-sion)是一類重要的亨澤爾擴張。藉助這類擴張,欲求賦值環在某個有限擴張上的拓展個數,只須考察此有限擴張到代數閉擴張中...
這一工作導致賦值論以及局部域理論的發展。他也是哈塞原理最早的奠基者,他的學生H.哈塞發展了進理論。亨澤爾和哈塞的“局部-整體原理”著稱於世。亨澤爾還是代數函式...
n亨澤爾賦值(n-Henselian valuation)一種特殊的賦值.賦值環滿足n亨澤爾條件的賦值.這種賦值又可作如下的刻畫:φ成為域F的一個。亨澤爾賦值,若且唯若對於F上任何...
牛頓多邊形(Newton's polygon)是一階亨澤爾域上多項式可約性的一種判別法。亨澤爾域亦稱亨澤爾賦值域。一種重要的賦值域。若φ是域F的一個亨澤爾賦值,則稱賦值域...
P 進數域又稱局部數域,它是數域關於進絕對值的完備化。進數域的研究和代數數論的局部化方法,均始於K.亨澤爾1902年的工作。...
