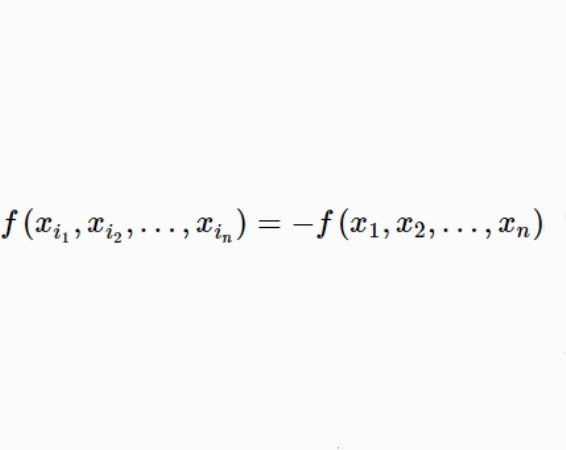交錯多項式

交錯多項式(alternating polynomial)是對稱多項式概念的推廣，設f是自由代數Λ{X}中含n個變元的一個多項式，t≤n為給定正整數，若f的每個單項式中x_i(1≤i≤t)出現且僅出現一次，稱f為t線性多項式。若對任意i，j，1≤i&_i代x_j後f(…，x_i，…，x_i，…)=0，則稱f為t交錯多項式。特別地，當n=t時，f稱為交錯多項式，若f是t線性又是t交錯多項式，則稱f為t正規多項式，特別地，當t=n時，稱f為正規多項式，例如，標準多項式Sn是正規的。

基本介紹

• 中文名：交錯多項式
• 外文名：alternating polynomial
• 所屬學科：數學
• 所屬問題：高等代數(多項式)
• 簡介：對稱多項式概念的推廣

基本介紹

設f(x₁，x₂，…，x_n)是數域F上關於變數x₁，x₂，…，x_n的n元多項式。如果對1，2，…，n的任意一個奇排列i₁i₂…i_n，都有

則f(x₁，x₂，…，x_n)叫做交錯多項式。例如，n個變數x₁，x₂，…，x_n之間的n(n-1)/2個差x_j-x_i(其中1≤i<j≤n)的乘積p(x_1，x₂，…，x_n)就是一個交錯多項式，這裡p(x₁，x₂，…，x_n)叫做最簡交錯多項式。

相關介紹

設f(x₁，x₂，…，x_n)是數域P上的n元多項式，若對於x₁，x₂，…，x_n的任意排列x_i1，x_i2，…，x_in，所有f(x_i1，x_i2，…，x_in)只能是兩個不同的多項式，則稱f(x₁，x₂，…，x_n)為關於x₁，x₂，…，x_n的交錯多項式，當這兩個不同的式子只能是f(x₁，x₂，…，x_n)與-f(x₁，x₂，…，x_n)時，稱f(x₁，x₂，…，x_n)為狹義交錯多項式.例如，f(x₁，x₂，x₃)=(x₂-x₁)(x₃-x₁)(x₃-x₂)+2x₁x₂x₃為關於x₁，x₂，x₃的交錯多項式，n元多項式(x₂-x₁)(x₃-x₁)…(x_n-x₁)為關於x₁，x₂，…，x_n的狹義交錯多項式，這個特殊的狹義交錯多項式稱為最簡交錯多項式，一個狹義交錯多項式與一個對稱多項式的和與積是交錯多項式。