二項方程

如果一元n次方程（n∈N﹢）的一邊只有含未知數的一項和非零的常數項，另一邊是零，那么這樣的方程就叫做二項方程。

基本介紹

• 中文名：二項方程
• 外文名：binomial equation
• 適用範圍：數理科學

定義

定義一

二項方程是一種特殊方程，指係數 a,b 均為非零常數的一元 n 次方程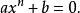

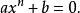
它的 n 個不同的複數根是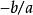 的 n 個 n 次方根；二項方程 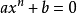至多有兩個實根

或其中之一。

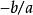
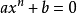
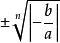
定義二

一種簡單的代數方程，指數域 P 上形如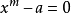 的方程。在複數域上，若以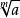表示它的一個根，則 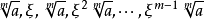是它的全部根，式中ξ 為 m 次本原單位根。實際上它們就是複數 a 在複數域內的全部 m 次方根。

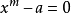
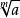
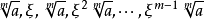
一般形式

關於x的一元n次二項方程的一般形式為axⁿ+b=0 ，其中n∈N_﹢，a,b均為常數項，且ab≠0。

註：axⁿ=0（a≠0，n∈N_﹢）不是二項方程。但它是非常特殊的n次方程，它有唯一的n重實根0。

解法

將原方程化為xⁿ=-b/a的形式後，用複數開n次方（n≥2，n∈N_﹢）的方法即可求解。它是用代數方法解一元n次方程的基礎。

二項方程的左邊只有兩項，其中一項含未知數x，這項的次數就是方程的次數；另一項是常數項；方程的右邊是0。

舉例

例1 解二項方程x³-1=0

解 將等號左邊常數項-1移到等號右邊，可得x³=1，

再根據複數開3次方的定義，可直接得出原方程的三個根為

x₁=1，x₂=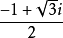 ，x₃= 。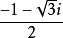

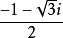
例2 解二項方程x⁴-16=0

解法1 （直接開方法）將等號左邊常數項-1移到等號右邊，可得x⁴=16，

再根據複數開4次方的定義，可直接得出原方程的四個根為

x₁=-2i，x₂=2i，x₃=-2，x₄=2。

解法2 （因式分解法）將等號左邊的二項式在R上因式分解，得（x²+4）（x²-4）=0，

再等號左邊的乘積在C上因式分解，得（x+2i）（x-2i）（x+2）（x-2）=0。

於是，要使原方程成立，等號左邊的四個因子至少有一個為0，

故x+2i=0，或x-2i=0，或x+2=0，或x-2=0。

這樣，就得到了原方程的四個根分別為x₁=-2i，x₂=2i，x₃=-2，x₄=2。