基本介紹
- 中文名:不等邊三角形
- 外文名:scalene triangle
- 概念:二或三條邊都不相等的三角形
- 學科:數理科學
- 類型:數學術語
- 三角形:三條線段‘首尾’順次連線的圖形
三角形


定義
若干“心”的一個性質
性質證明:
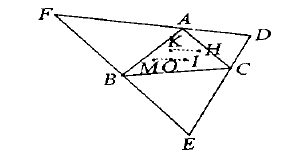




常見的三角形按邊分有不等邊三角形,等腰三角(腰與底不等的等腰三角形、腰與底相等的等腰三角形即等邊三角形)。不等邊三角形,數學定義,指的是三條邊都不相等的...
一種少見的三角形票形,郵票的三邊邊長各不相等。僅見哥倫比亞於1869—1870年發行過此票,郵票為三邊不相等的直角三角形,紫色,面值2.5分。 ...
三角形是由同一平面內不在同一直線上的三條線段‘首尾’順次連線所組成的封閉圖形,在數學、建築學有套用。常見的三角形按邊分有普通三角形(三條邊都不相等),...
事實上,以萊洛三角形為例,只需經過如下的“處理”,就可以作出與其相應沒有任何尖角頂的光滑的新的等寬曲線。把等邊三角形的各邊向兩個方向 延長相等的一段;以...
1865年,哥倫比亞發行一種獨特的不等邊三角形郵票,其底角一作50度,一作40度。200年後,法屬非洲殖民地奧博克忽又發行兩種 等邊三角形郵票。以後各國都起而仿效,有...
拉格朗日點中位於兩較大質量的質點相互繞轉平面上並與它們構成等邊三角形。...... 拉格朗日點中位於兩較大質量的質點相互繞轉平面上並與它們構成等邊三角形。...
三角形是由同一平面內不在同一直線上的三條線段‘首尾’順次連線所組成的封閉圖形,在數學、建築學有套用。常見的三角形按邊分有普通三角形(三條邊都不相等),...
三角形面積公式是指使用算式計算出三角形的面積,同一平面內,且不在同一直線的三條線段首尾順次相接所組成的封閉圖形叫做三角形,符號為△。常見的三角形按邊分有...
等邊三角形(又稱正三邊形),為三邊相等的三角形,其三個內角相等,均為60°,它是銳角三角形的一種。等邊三角形也是最穩定的結構。等邊三角形是特殊的等腰三角形...
在一個正方形里畫一個等邊三角形(邊為正方形邊長,但不與正方形的邊長重合),然後以三角形的每個邊長頂點為圓心,作一條連線另外兩個頂點的弧。然後,你就得到了...
報備機構:江蘇維納文化傳媒有限公司 2015 年3 月 許可證號: (蘇)字第00691號 劇名題材 體裁 集數 拍攝日期 製作周期 一般 喜劇 戲曲 愛情等邊三角形 當代都市...
等腰三角形中,相等的兩條邊稱為這個三角形的腰,另一邊叫做底邊。兩腰的夾角叫做頂角,腰和底邊的夾角叫做底角。等腰三角形的兩個底角度數相等(簡寫成“等邊對等角...
