基本介紹
- 中文名:不可分量原理
- 外文名:Uncomponent principle
- 拼音:Bù kě fèn liàng yuán lǐ
- 隸屬:數理科學
- 提出者:Cavalieri
- 別名:卡瓦列利原理
來源,原理,推論,實例,套用,
來源
義大利數學家Cavalieri,Francesco Bonaventure(1598 ~ 1647)在《用新的方法推進連續體的不可分量的幾何學》(1635)提出“不可分量原理”:線段是無數個等距點構成,面積是無數個等距平行線段構成,體積是無數個等距平行平面構成,這些點、線段、平面是長度、面積、體積的“不可分量”。Cavalieri 利用這種“不可分量”,進行長度、面積、體積的計算及其相關的推理,但是,他未能對“不可分量”作出嚴格的論述。數學家們對此褒貶不一。1644年, Cavalieri本人發現了關於“不可分量”的悖論。“不可分量原理”(義大利卡瓦列里,1635年)第一次給出了積分的一般方法。
原理
第一原理:有兩個平面片處於兩條平行線之間,在這兩個平面片內作任意平行於這兩條平行線的直線,如果它們被平面片所截得的線段長度相等,則這兩個平面片的面積相等。
推論
推論1. 夾在兩個平行平面問的兩個幾何體,被平行於這兩個平面的任意平面所截,如果截得的兩個截面的面積比總為m:n,那么這兩個幾何體的體積之比亦為m:n。
推論2.夾在兩條平行線間的兩個平面圖形,被平行於這兩條平行線的任意直線所截,如果截得的兩條線段的長度之比總為m:n,那么這兩個平面圖形的面積之比亦為m:n。
實例
對於被置於同一個直角坐標繫上的橢圓和圓: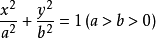 ;
; 。
。
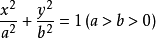

從上述每一個方程中解出y,得到 ;
;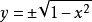 。
。

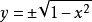
由此看出:橢圓和圓的對應的縱坐標之比為b/a。這就意味著,橢圓和圓的對應垂直弦之比是b/a;根據卡瓦列里不可分量的第一個原理,有橢圓和圓的面積之比也是b/a。
套用
案例教學法是教師本著理論與實踐有機結合的教育理念,根據教學目的和要求,通過向學生提供記錄實際發生的情況或事件案例,採用在師生之間、生生之間的多向互動、平等對話和積極研討等形式,培養和發展學生主動參與課堂討論,提高學生面對複雜教育情境的決策能力和行動能力的一系列教學方式的總和。
在不可分量原理的教學中,可以採用案例教學法,通過具體案例讓學生明確不可分量原理的基本內容和推理。以此來發展學生的積極思維,培養其綜合分析能力及創新能力,同時取得了良好的教學效果。

