上下文無關文法

在計算機科學中，形式語言是：某個字母表上，一些有限長字串的集合，而形式文法是描述這個集合的一種方法。形式文法之所以這樣命名，是因為它與人類自然語言中的文法相似的緣故。

形式文法描述形式語言的基本想法是，從一個特殊的初始符號出發，不斷的套用一些產生式規則，從而生成出一個字串的集合。產生式規則指定了某些符號組合如何被另外一些符號組合替換。

最常見的文法的分類系統是諾姆·喬姆斯基於1956年發展的喬姆斯基譜系，這個分類譜系把所有的文法分成四種類型：無限制文法、上下文相關文法、上下文無關文法和正規文法。四類文法對應的語言類分別是遞歸可枚舉語言、上下文相關語言、上下文無關語言和正規語言。

基本介紹

• 中文名：上下文無關文法
• 外文名：context-free grammar
• 縮寫：CFG

簡介

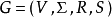
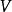
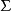
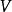
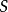
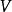
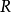
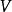
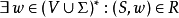
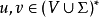
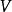
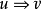
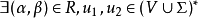
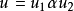
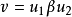
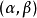
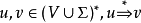
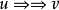
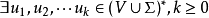
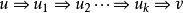
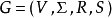
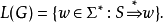
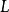
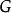
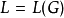
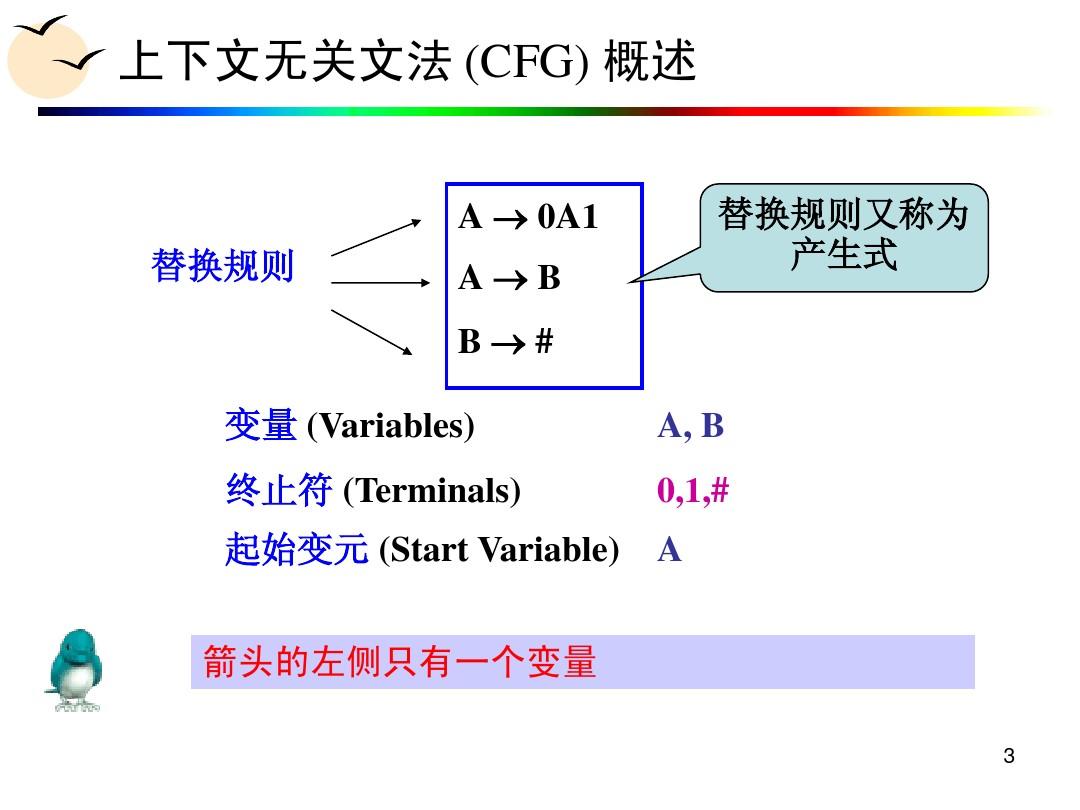
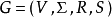
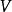
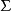
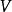
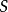
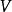
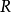
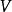
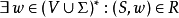
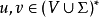
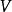
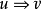
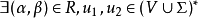
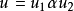
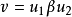
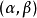
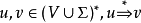
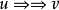
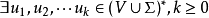
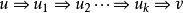
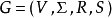
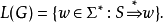
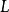
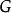
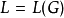
上下文無關文法（英語：context-free grammar，縮寫為CFG），在計算機科學中，若一個形式文法G = (N, Σ, P, S) 的產生式規則都取如下的形式：V->w，則謂之。其中 V∈N ，w∈(N∪Σ)* 。上下文無關文法取名為“上下文無關”的原因就是因為字元 V 總可以被字串 w 自由替換，而無需考慮字元 V 出現的上下文。一個形式語言是上下文無關的，如果它是由上下文無關文法生成的（條目上下文無關語言）。

上下文無關文法重要的原因在於它們擁有足夠強的表達力來表示大多數程式設計語言的語法；實際上，幾乎所有程式設計語言都是通過上下文無關文法來定義的。另一方面，上下文無關文法又足夠簡單，使得我們可以構造有效的分析算法來檢驗一個給定字串是否是由某個上下文無關文法產生的。例子可以參見LR 分析器和LL 分析器。

BNF（巴克斯-諾爾範式）經常用來表達上下文無關文法。

形式定義

上下文無關文法G是 4-元組：

這裡的

1.是“非終結”符號或變數的有限集合。它們表示在句子中不同類型的短語或子句。

2.是“終結符”的有限集合，無交集於，它們構成了句子的實際內容。

3. 是開始變數，用來表示整個句子（或程式）。它必須是的元素。

4. 是從到 的關係，使得。

此外，是有限集合。的成員叫做文法的“規則”或“產生式”。星號表示Kleene星號運算。

補充定義 1

對於任何字元串，我們稱生成，寫為 ，如果 使得 且。因此v是套用規則 於的結果。

補充定義 2

對於任何（或在某些教科書中），如果使得。

補充定義 3

文法的語言是集合

補充定義 4

語言被稱為是上下文無關語言（CFL），如果存在一個 CFG 使得。

範式

每一個不生成空串的上下文無關文法都可以轉化為等價的Chomsky 範式或Greibach 範式。這裡兩個文法等價的含義指它們生成相同的語言。

由於 Chomsky 範式在形式上非常簡單，所以它在理論和實踐上都有套用。比如，對每一個上下文無關語言，我們可以利用 Chomsky 範式構造一個多項式算法，用它來判斷一個給定字串是否屬於這個語言（CYK算法）。

參見

• 上下文有關文法
• 形式文法
• 分析
• 分析表達式文法
• 隨機上下文無關文法