基本介紹
- 中文名：CYK算法
- 外文名：Cocke–Younger–Kasami algorithm
簡介,相關參數定義,算法描述,簡介,偽代碼,擴展CYK算法,簡介,偽代碼,
簡介
普通的回溯法（backtracking）在最壞的情況下需要指數時間才能解決這樣的問題，而CYK算法只需要多項式時間就夠了（{\displaystyle ~O(n^{3})}， n 為字元串 w 的長度）。CYK算法採用了動態規劃的思想。
對於一個任意給定的上下文無關文法，都可以使用CYK算法來計算上述問題，但首先要將該文法轉換成喬姆斯基範式。
相關參數定義
1.
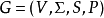是一個上下文無關文法
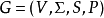
2.對於任意字元串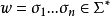
，定義
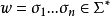
3.對於任意選擇的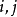
，定義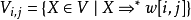
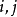
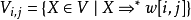
算法描述
簡介
通過由下而上的方法計算
這個集合，如果
，那么就說明
是被上下文無關文法G接受的字元串。
因為
是一個喬姆斯基範式，若且唯若有下面描述的情況時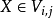
：
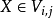
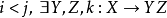
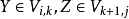
偽代碼
FOR i:= 1 TO n DO {\displaystyle V_{i,i}:=\{X\in V~|~X\rightarrow \sigma _{i}~in~P\}}FOR l:= 1 TO n-1 FOR i:= 1 TO n-l DO {\displaystyle ~V_{i,i+l}:=\varnothing } FOR k:= i TO i+l-1 DO {\displaystyle ~V_{i,i+l}:=V_{i,i+l}\cup \{X~|~X\rightarrow YZ,Y\in V_{i,k},Z\in V_{k+1,i+l}\}}IF {\displaystyle S\in V_{1,n}} THEN accept ELSE reject擴展CYK算法
簡介
對於上述CYK算法作一個小改動，也就是說記住每次的k，就可以自動產生一個由該上下文無關語言的推導樹。
偽代碼
FOR i:= 1 TO n DO {\displaystyle V_{i,i}:=\{X\in V~|~X\rightarrow \sigma _{i}~in~P\}}FOR l:= 1 TO n-1 FOR i:= 1 TO n-l DO {\displaystyle ~V_{i,i+l}:=\varnothing } FOR k:= i TO i+l-1 DO {\displaystyle ~V_{i,i+l}:=V_{i,i+l}\cup \{(X,k)~|~X\rightarrow YZ,Y\in V_{i,k},Z\in V_{k+1,i+l}\}}IF {\displaystyle \exists k:(S,k)\in V_{1,n}} THEN accept ELSE reject通過對下面的方法遞歸運行就可以生成推導樹。Tree(X,i,j): IF i=j THEN RETURN {\displaystyle ~\sigma _{i}} 選擇一個 k 使 {\displaystyle (X,k)\in V_{i,j}} 選擇 Y 和 Z 使 {\displaystyle X\rightarrow YZ,Y\in V_{i,k},Z\in V_{k+1,j}} RETURN Tree(X,Tree(Y,i,k),Tree(Z,k+1,j))