基本介紹
- 中文名:無限制文法
- 又稱:0型文法
- 學科:數學
簡介,形式定義,無限制文法和圖靈機,計算性質,
簡介
形式定義
無限制文法是形式文法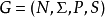 ,這裡的N是非終結符的集合,
,這裡的N是非終結符的集合, 是終結符的集合,這裡的
是終結符的集合,這裡的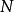 和
和 是無交集的(實際上這個限制不是必需的,因為無限制文法在非終結符和終結符之間不做真實區分,存在這個指定純粹是為了使得你在嘗試生成文法的句子形式的時候知道何時停止),P是形如
是無交集的(實際上這個限制不是必需的,因為無限制文法在非終結符和終結符之間不做真實區分,存在這個指定純粹是為了使得你在嘗試生成文法的句子形式的時候知道何時停止),P是形如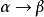 的產生規則的集合,這裡的
的產生規則的集合,這裡的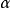 和
和 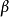 是在 中的符號的字元串而
是在 中的符號的字元串而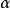 是非空字元串,
是非空字元串,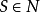 是特別指定的開始符號。如名稱所暗含的,在無限制文法可以有什麼類型的產生規則上沒有真實限制。
是特別指定的開始符號。如名稱所暗含的,在無限制文法可以有什麼類型的產生規則上沒有真實限制。

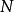

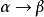
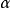
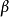
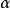
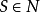
無限制文法和圖靈機
可以證明無限制文法特徵化了遞歸可枚舉語言。這同於聲稱對於所有無限制文法G都存在某個圖靈機有能力識別 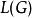 反之亦然。給定一個無限制文法,這種圖靈機足夠簡單構造為兩磁帶非確定圖靈機。第一個磁帶包含要被測試的輸入字W,而機器使用第二個磁帶生成來自G的句子形式。圖靈機接著做如下事情:
反之亦然。給定一個無限制文法,這種圖靈機足夠簡單構造為兩磁帶非確定圖靈機。第一個磁帶包含要被測試的輸入字W,而機器使用第二個磁帶生成來自G的句子形式。圖靈機接著做如下事情:
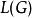
開始於第二個磁帶的左端並重複的選定要右移或選擇在磁帶上的當前位置。
非確定的從G中選定一個產生式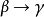 。
。
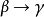
如果 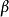 出現在第二個磁帶的某個位置,在這個點上把
出現在第二個磁帶的某個位置,在這個點上把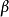 替代為
替代為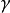 ,依據
,依據 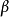 和 的相對長度可能要把在磁帶上的符號向左或右移動(就是說如果
和 的相對長度可能要把在磁帶上的符號向左或右移動(就是說如果 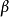 長於
長於  ,左移磁帶符號)。
,左移磁帶符號)。
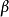
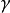
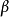
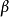

比較在磁帶 2 上的結果句子形式和在磁帶 1 上的字。如果匹配,則圖靈機接受這個字。如果不匹配則回到步驟 1。
容易看出這個圖靈機將在最後步驟被執行任意次之後在第二個磁帶上生成G的所有的句子形式,所以語言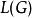 必定是遞歸可枚舉的。
必定是遞歸可枚舉的。
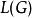
相反構造也是可能的。給定某個圖靈機,有可能建立一個無限制文法。
計算性質
從無限制文法和圖靈機的等價性上,給定一個字元串 是否屬於某個無限制文法的語言的決定性問題一般是不可判定的。
是否屬於某個無限制文法的語言的決定性問題一般是不可判定的。

