基本介紹
- 中文名:遞歸可枚舉語言
- 又名:部分可判定語言
- 性質:形式語言類型
- 領域:計算機
形式定義
定義

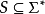



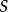
兩個定義的等價性
- 運行E,依次生成字元串s1,s2, ...;
- 若遇到某個si= ω則進入接受狀態並停機。
- 對i= 1, 2, 3, ...重複下列步驟;
- 設Σ= {s1,s2, ...},分別將s1,s2, ... ,si作為M的輸入,模擬M執行i步;
- 若某個sj, 1 ≤ j ≤ i,在i步內可被M接受,則將其輸出。
閉包性質
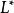

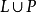
圖靈可識別語言與圖靈可判定語言的關係
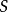








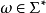


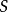

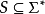



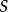
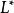

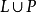
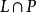








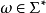


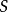
在數學、邏輯和計算機科學中,遞歸可枚舉語言是也叫做部分可判定語言或圖靈可識別語言的形式語言類型。它在形式語言的喬姆斯基層級中叫做類型-0語言。所有遞歸可枚舉...
遞歸可枚舉集合(英語:Recursively enumerable set)是可計算性理論或更狹義的遞歸論中的一個概念。可數集合S被稱為是遞歸可枚舉、計算可枚舉的、半可判定的或可證明...
0型文法是形式語言譜系中最大的文法類。由0型文法產生的形式語言恰是圖靈機所識別的語言類,即遞歸可枚舉語言。②1型文法。又稱為上下文有關文法。這種文法要求...
在數學、邏輯和計算機科學中,遞歸可枚舉語言是也叫做部分可判定語言或圖靈可識別語言的形式語言類型。它在形式語言的喬姆斯基層級中叫做類型-0語言。所有遞歸可枚舉...
在形式語言理論中,無限制文法是對文法的產生式左右兩側都沒有限制的形式文法。這是喬姆斯基層級中最一般性的文法類,它們可以識別任意的遞歸可枚舉語言。...
萊斯定理(Rice's theorem)是可計算性理論中的一條定理,由亨利·戈登·萊斯於...遞歸可枚舉語言的所有非平凡(nontrival)性質都是不可判定的。“非平凡”是指,...
可被圖靈機識別的語言是指能夠使圖靈機停機的字串,這類語言又被稱為遞歸可枚舉語言。注意遞歸可枚舉語言與遞歸語言的區別,後者是前者的一個真子集,是能夠被一個...
這樣我們可以定義可計算性等級:所有的語言的集合,記為All;遞歸可枚舉語言,即可以被圖靈機枚舉的語言的集合,記為RE;遞歸語言,即可以被圖靈機決定的語言的集合,記...
這樣我們可以定義可計算性等級:所有的語言的集合,記為All;遞歸可枚舉語言,即可以被圖靈機枚舉的語言的集合,記為RE;遞歸語言,即可以被圖靈機決定的語言的集合,記...
這樣我們可以定義可計算性等級:所有的語言的集合,記為All;遞歸可枚舉語言,即可以被圖靈機枚舉的語言的集合,記為RE;遞歸語言,即可以被圖靈機決定的語言的集合,記...
可計算枚舉語言被命名為0-型語言,上下文相關語言被命名為1-型語言,上下文無關語言被命名為2-型語言,正則語言被命名為3-型語言。低型語言不是高型的,默認情況下...
該類型的文法能夠產生所有可被圖靈機識別的語言。可被圖靈機識別的語言是指能夠使圖靈機停機的字串,這類語言又被稱為遞歸可枚舉語言。注意遞歸可枚舉語言與遞歸語言...
圖靈機判定遞歸語言並識別遞歸可枚舉語言。自動機能力判定 編輯 確定有限狀態自動機與非確定有限狀態自動機識別的語言都是正則語言。由於正則語言的良好性質,許多為...
四類文法對應的語言類分別是遞歸可枚舉語言、上下文相關語言、上下文無關語言和正規語言。中文名 上下文無關文法 外文名 context-free grammar 縮寫 CFG ...
圖靈可判定語言遞歸可枚舉語言 可計算函式遞歸函式停機問題 可判定性不可判定性 圖靈機等價機器 編輯 除了圖靈機以外,人們還發明了很多其它的計算模型。包括:...
確定上下文無關文法是確定下推自動機可識別的文法。確定上下文無關語言是確定...四類文法對應的語言類分別是遞歸可枚舉語言、上下文相關語言、上下文無關語言和...
這樣我們可以定義可計算性等級:所有的語言的集合,記為All;遞歸可枚舉語言,即可以被圖靈機枚舉的語言的集合,記為RE;遞歸語言,即可以被圖靈機決定的語言的集合,記...
可計算枚舉語言被命名為0-型語言,上下文相關語言被命名為1-型語言,上下文無關語言被命名為2-型語言,正則語言被命名為3-型語言。低型語言不是高型的,默認情況下...
在理論計算機科學中,帕里克定理指出,對於上下文無關語言,如果只關心其中每個終止...四類文法對應的語言類分別是遞歸可枚舉語言、上下文相關語言、上下文無關語言和...
4.2遞歸可枚舉語言的形式表達 習題 第5章計算複雜類 5.1複雜類 5.2分離定理 5.3可達性方法 習題 第6章歸約和完備性 6.1歸約 6.2完備性 6.3...
實際上,在波斯特系統中,可以限定所有的產生式都形如uA->Aw,其中A為變元,u,wE乏‘,並約定只有一條初始假設,它們仍能產生所有遞歸可枚舉的語言。即對波斯特系統...
或者說,任何0型文語言都是遞歸可枚舉的,反之,遞歸可枚舉集必定是一個0型語言。0型文法是這幾類文法中,限制最少的一個,所以我們在試題中見到的,至少是0型...
