格雷巴赫標準式

在計算機科學中，聲稱一個上下文無關文法是Greibach 標準式(範式)(GNF)的意味著所有的產生規則都有如下形式: A->αX或 s->ε 這裡的 A 是非終結符，α 是終結符，X 是不包括開始符號的非終結符的(可能為空)的序列，S 是開始符號，而 ε 是空串。

基本介紹

• 中文名：格雷巴赫標準式
• 學科：計算機

定義

在計算機科學中，聲稱一個上下文無關文法是Greibach 標準式（範式）(GNF)的意味著所有的產生規則都有如下形式：

或

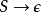
這裡的A是非終結符，α 是終結符，X是不包括開始符號的非終結符的（可能為空）的序列，S是開始符號，而ε是空串。

可觀察出這種文法沒有左遞歸。

所有上下文無關文法口可以被轉換成等價的 Greibach 範式的文法。（某些定義不認可第二種形式的規則，在這種情況下能生成空串的上下文無關文法不能被如此轉換。）這可以被用來證明所有上下文無關語言可以被非確定下推自動機所接受。

給定 GNF 的一個文法和長度為n的符合這個文法的一個可導出的字元串，任何自頂向下分析器將在深度n停機。

Greibach 範式得名於Sheila Greibach。

範例

請寫出S->AA|0 A->SS|1 的 Greibach 標準式A¹→A²A²|0 A²→A¹A¹|1

A¹→A²A²|0 A²→A²A²A¹|0A¹|1

A¹→A²A²|0 A²→0A¹|1|0A¹B²|1B² B²→A²A¹|A²A¹B²

A¹→0A¹A²|1A²|0A¹B²A²|1B²A²|0 A²→0A¹|1|0A¹B²|1B² B²→A²A¹|A²A¹B²

A¹→0A¹A²|1A²|0A¹B²A²|1B²A²|0 A²→0A¹|1|0A¹B²1B² B²→0A¹A¹|0A¹B²A¹|1B²A¹|0A¹A¹B²|0A¹B²A¹B²|1B²A¹B²|1A¹|1A¹B²

上下文無關文法

在 計算機科學中，若一個形式文法G = (N, Σ, P, S) 的 產生式規則都取如下的形式：V -> w，則稱之為上下文無關的，其中 V∈N ，w∈(N∪Σ)* 。上下文無關文法取名為“上下文無關”的原因就是因為字元 V 總可以被字串 w 自由替換，而無需考慮字元 V 出現的上下文。一個形式語言是上下文無關的，如果它是由上下文無關文法生成的﹙條目上下文無關語言﹚。

上下文無關文法重要的原因在於它們擁有足夠強的表達力來表示大多數程式設計語言的語法；實際上，幾乎所有程式設計語言都是通 過上下文無關文法來定義的。另一方面，上下文無關文法又足夠簡單，使得我們可以構造有效的分析算法來檢驗一個給定字串是否是由某個上下文無關文法產生的。例子可以參見 LR 分析器和 LL 分析器。