計算方法
直接計算——對角線法
標準方法是在已給行列式的右邊添加已給行列式的第一列、第二列。我們把行列式的左上角到右下角的
對角線稱為主對角線,把右上角到左下角的對角線稱為次對角線。這時,三階行列式的值等於
主對角線的三個數的積與和主對角線平行的對角線上的三個數的積的和減去次對角線的三個數的積與和次對角線平行的對角線上三個數的積的和的差。
任何一行或一列展開——代數餘子式
行列式某元素的餘子式:行列式划去該元素所在的行與列的各元素,剩下的元素按原樣排列,得到的新行列式.
行列式某元素的代數餘子式:行列式某元素的餘子式與該元素對應的正負符號的乘積.
即行列式可以按某一行或某一列展開成元素與其對應的代數餘子式的乘積之和。
 三階行列式運算
三階行列式運算舉例
結果為 a1·b2·c3+b1·c2·a3+c1·a2·b3-a3·b2·c1-b3·c2·a1-c3·a2·b1(注意對角線就容易記住了)
這裡一共是六項相加減,整理下可以這么記:
a1(b2·c3-b3·c2) - a2(b1·c3-b3·c1) + a3(b1·c2-b2·c1)=
a1(b2·c3-b3·c2) - b1(a2·c3 - a3·c2) + c1(a2·b3 - a3·b2)
此時可以記住為:
a1*(a1的餘子式)-a2*(a2的餘子式)+a3*(a3的餘子式)=
a1*(a1的餘子式)-b1*(b1的餘子式)+c1*(c1的餘子式)
某個數的
餘子式是指刪去那個數所在的行和列後剩下的行列式。
行列式的每一項要求:不同行不同列的數字相乘
如選了a1則與其相乘的數只能在2,3行2,3列中找,(即在 b2 b3 c2c3中找)
而a
1(b
2·c
3-b
3·c
2) - a
2(b
1c
3-b
3·c
1) + a
3(b
1·c
2-b
2·c
1)是用了行列式展開運算:即行列式等於它第一行的每一個數乘以它的
餘子式,或等於第一列的每一個數乘以它的
餘子式,然後按照 + - + - + -......的規律給每一項添加符
號之後再做求和計算。
性質
性質1 行列式與它的轉置行列式相等。
性質2 互換行列式的兩行(列),行列式變號。
推論 如果行列式有兩行(列)完全相同,則此行列式為零。
性質3 行列式的某一行(列)中所有的元素都乘以同一數k,等於用數k乘此行列式。
推論 行列式中某一行(列)的所有元素的公因子可以提到行列式符號的外面。
性質4 行列式中如果有兩行(列)元素成比例,則此行列式等於零。
性質5 把行列式的某一列(行)的各元素乘以同一數然後加到另一列(行)對應的元素上去,行列式不變。
套用
求三角形面積
三階行列式:三階行列式的展開式也可用對角線法則得到,三階行列式的對角線法則如下圖所示:
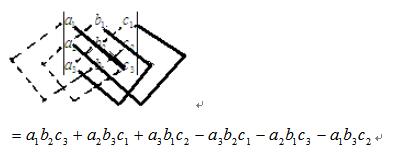 三階行列式的對角線法則
三階行列式的對角線法則三角形的面積求法
求兩個矩陣相乘
方法1:
把兩個行列式,都分別求出來,然後相乘
方法2:
矩陣A乘矩陣B,得矩陣C,方法是A的第一行元素分別對應乘以B的第一列元素各元素,相加得C11,A的第一行元素對應乘以B的第二行各元素,相加得C12,以此類推,C的第二行元素為A的第二行元素按上面方法與B相乘所得結果,以此類推.N階矩陣都是這樣乘,A的列數要與B的行數相等.

 三階行列式運算
三階行列式運算
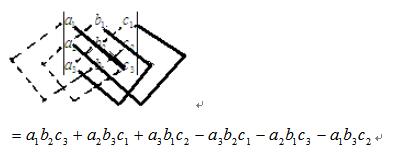 三階行列式的對角線法則
三階行列式的對角線法則


