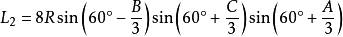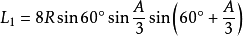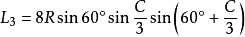定義
三等分角線(Trisectrix)是可以用來三等分任意角的曲線。
性質
三角形有關角三等分線的交點構成的三角形有許多美妙的性質。
定理一:與任意△ABC每邊相鄰的每兩個
優角相鄰的三等分線的反向延長線的交點構成正三角形,且其邊長為
。
定理二:三角形任意一個優角與另兩個
劣角中,與每邊相鄰的每兩個角相鄰的三等分線(或其反向延長線)的交點構成正三角形,且邊BC、AC、AB所正對的正三角形的邊長分別是:
定理三:任意△ABC任意一邊相鄰的兩個優角相鄰三等分線的反向延長線的交點,及與這邊相鄰的劣角與外角相鄰的三等分線(或其反向延長線)的交點構成正三角形,且邊BC、AB、AC所正對的三角形的邊長分別是:
定理四:任意△ABC任意一邊相鄰的兩個外角相鄰三等分線的交點,及與這邊相鄰的劣角與優角相鄰三等分線(或其反向延長線)的交點構成正三角形,且點A、B、C所對的正三角形的邊長分別是:
定理五:任意△ABC沒有公共頂點的任意一個劣角、一個優角及其夾邊所對的另兩個外角中,與每邊相鄰的每兩個角相鄰的三等分線(或其反向延長線)的交點構成正三角形,且六個正三角形的邊長分別是:
定理六:任意△ABC任意兩個優角及其夾邊所對的兩個外角中,與每邊相鄰的每兩個角相鄰的三等分線(或其反向延長線)的交點構成正三角形,且邊BC、AB、AC所對的正三角形的邊長分別是:
定理七:任意一邊相鄰的兩個劣角的相鄰三等分線的交點,及與這邊相鄰的優角與外角的相鄰三等分線的交點構成正三角形,且點A、B、C所對的正三角形的邊長分別是:
類型
蝸牛三等分角線(有些文獻直接稱此曲線為三等分角線)
馬克勞林三等分角線
等邊三葉(Equilateraltrefoil)
契爾恩豪森三次曲線
丟勒的大青葉(Durer'sfolium)
三次拋物線(Cubicparabola)
偏心率為2的
雙曲線三葉的
玫瑰線拋物線相關曲線
與三等分角線相關的曲線是等分角線(sectrix),是可以將任意角分為整數個的曲線。以下是一些等分角線:
阿基米德螺線割圓曲線馬克勞林等分角線
Ceva等分角線(SectrixofCeva)
Delanges等分角線(SectrixofDelanges)